Определить годовые нагрузочные потери электроэнергии следующими методами
К двухцепной линии электропередачи напряжением U = 110 кВ длиной L = 40 км, выполненной маркой провода АС 120/19, подключена нагрузка, режим работы которой характеризуется годовым графиком нагрузки по продолжительности, приведенным в табл. 9.5. Наибольшая передаваемая активная мощность РНБ = 60 МВт.
Таблица 9.5
Характеристика годового графика нагрузки по продолжительности
| Номера ступеней графика | ||||
| Величина нагрузки в долях от наибольшей передаваемой активной мощности | 1,0 | 0,80 | 0,60 | 0,40 |
| Длительность ступеней, ч | ||||
| Коэффициент мощности | 0,90 | 0,85 | 0,82 | 0,79 |
Определить годовые нагрузочные потери электроэнергии следующими методами:
- характерных режимов;
- среднеквадратичных параметров;
- времени наибольших потерь;
- раздельного времени наибольших потерь;
- средних нагрузок.
Вычислить различия в потерях энергии (в процентах) по различным методам, приняв за эталонный метод характерных режимов.
Решение
Для заданной марки провода найдем из справочника удельное активное сопротивление rо = 0,27 Ом/км. Сопротивление одной цепи R, = r0L = 0,27*40 = 10,8 Ом, а двух параллельных цепей R = 0,5R1 = 0,5-10,8 = 5,4 Ом.
Для вычисления потерь электроэнергии по методу характерных режимов воспользуемся формулой (9.14), приняв в качестве характерных режимов каждую из ступеней заданного годовогографика нагрузки по продолжительности

где ΔРj — потери мощности при нагрузке Pj j-й ступени графика нагрузки по продолжительности; Δt j —длительность j-й ступени.
На каждой ступени графика потери мощности найдем по формуле:

В результате получим:

На основании графика нагрузки по продолжительности определим энергию, переданную по линии
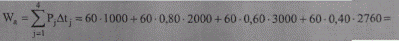
= 330240 МВт ч
Тогда потери электроэнергии в процентах от передаваемой мощности составят
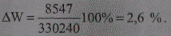
Из графика нагрузки по продолжительности определим время использования наибольшей активной мощности и наибольшей полной мощности


Для определения потерь электроэнергии по методу среднеквадратичных параметров сначала из графика нагрузки по продолжительности найдем среднеквадратичную мощность:
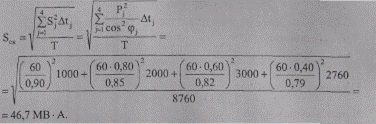
Среднеквадратичный ток
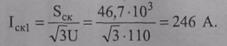
Тогда годовые потери электроэнергии по формуле (9.26)
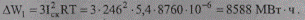
Погрешность относительно результата по методу характерных режимов составляет:
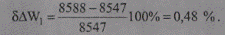
Найдем значение тока в режиме наибольших нагрузок

Определим среднеквадратичный ток по формуле (9.23):
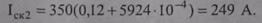
Тогда потери электроэнергии
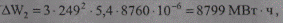
а погрешность
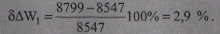
Таким образом, использование эмпирической формулы (9.23) приводит к большей погрешности, чем при вычислении среднеквадратичного тока по графику нагрузки.
Вычислим также среднеквадратичный ток по формуле (9.24). Для этого найдем сначала по формуле (9.18) коэффициент формы графика нагрузки
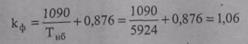
и по формуле (9.25) значение среднего тока. Активная энергия была вычислена ранееWa= 330240 МВт*ч. «Реактивную энергию» найдем так:
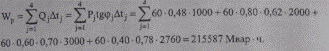
Тогда средний ток
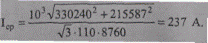
Среднеквадратичный ток

Потери электроэнергии

а погрешность

Таким образом, можно сделать вывод о том, что вычисление среднеквадратичного тока различными способами привело к приемлемым погрешностям определения потерь электроэнергии по сравнению с методом характерных режимов, принятым за эталонный.
Перейдем теперь к определению потерь энергии по методу времени наибольших потерь различными способами.
На основании заданного графика нагрузки по продолжительности
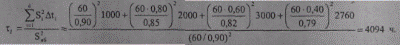
По эмпирической формуле (9.31)
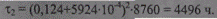
По зависимостям, приведенным на рис. 9.2, при ТНБ = 5924 ч и при cosφ в интервале от 0,90 до 0,79 (примем cosφ = 0,85) τ3 = 4200 ч.
По формуле (9.32) при вычисленном ранее Тн6 а = 5504 ч и заданных в графике нагрузки по продолжительности РНБ = 60 МВт, РНМ = 60 • 0,40 = 24 МВт

Тогда по формуле (9.34) найдем соответственно годовые потери электроэнергии:
.=40941

Погрешности вычислений относительно эталонного метода соответственно составят:

Как видно, вычисление времени наибольших потерь различными способами привело к разным, но вполне допустимым погрешностям. Наибольшая погрешность оказалась при использовании формулы (9.32), поэтому она и рекомендуется для оценки потерь лишь в проектных расчетах, когда достоверность исходной информации меньше, чем в условиях эксплуатации.
Определим теперь потери электроэнергии по методу раздельного времени наибольших потерь. Как видно из табл. 9.5, графики нагрузки активной и реактивной мощностей не идентичны, так как коэффициент мощности изменяется во времени. Найдем реактивную мощность для каждой ступени графика, используя формулу
| Номер ступени графика нагрузки | ||||
| Активная мощность, МВт | ||||
| Реактивная мощность, Мвар |
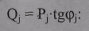
Отсюда следует, что максимумы активной и реактивной нагрузки также не совпадают во времени.
На основе формул (9.36) по графикам нагрузки найдем время наибольших потерь от передачи активной и реактивной мощности:
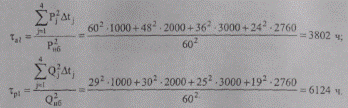
Потери электроэнергии определим по формуле (9.38):
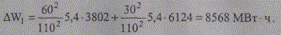
Найдем погрешность расчета относительно эталонного метода:
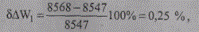
т. е. погрешность оказалась минимальной, зависящей лишь от точности вычислений.
Вычислим время наибольших потерь по эмпирическим формулам (9.40) и (9/41) при найденном ранее значении Тн6 а = 5504 ч и коэффициенте

Тогда потери электроэнергии

Погрешность расчета

Как и следовало ожидать, погрешность вычислений по эмпирическим формулам выше, чем по графикам нагрузки, но тем не менее она невелика.
Перейдем к вычислению потерь электроэнергии по методу средних нагрузок. Для этого определим сначала средние активную и реактивную мощности по вычисленным ранее значениям активной Wa=330240 МВт ч и «реактивной» WP=215587 Мвар ч энергии:


Тогда готовые потери электроэнергии по формуле (9.17) при вычисленном ранее коэффициенте формы графика нагрузки kф=1,06
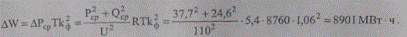
Погрешность относительно эталонного метода

Определим средние нагрузки приближенно по формулам (9.16)
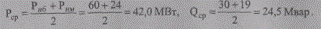
Тогда при этих нагрузках потери энергии

Погрешность

Как и следовало ожидать, приближенное вычисление средних нагрузок приводит к достаточно большой погрешности расчета потерь энергии.
ЗАДАЧА 9.2
Задана схема сети напряжением 10 кВ, приведенная на рис. 9.6, и параметры сети: длины, участков сети, км, их марки проводов и номинальные мощности трансформаторов 10/0,38 кВ, кВ*А. Ток головного участка в режиме наибольших нагрузок IГУ = 30 А. Время использования наибольшей нагрузки всех потребителей, подключенных к сети,
ТНБ = 4500 ч.
Определить годовые потери электроэнергии методом эквивалентного сопротивления и вероятностно-статистическим методом.

Рис. 9.6. Схема сети с исходными параметрами
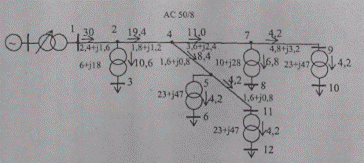
Рис. 9.7. Схема сети с сопротивлениями участков и токораспределением
Решение
По заданным номинальным мощностям трансформаторов, используя паспортные данные, найдем их активные и реактивные сопротивления. По заданным маркам проводов из справочников находим их удельные сопротивления r0 и х0. По заданным длинам участков найдем их активные и реактивные сопротивления. Результаты представлены на рис. 9.7.
Известную нагрузку головного участка распределим пропорционально номинальным мощностям трансформаторов, подключенных к сети. Так, ток трансформатора 23

где суммарная номинальная мощность трансформаторов
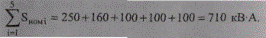
Используя первый закон Кирхгофа, найдем токи на всех участках. Результаты представлены на рис. 9.7.
По формулам (9.42) и (9.43) найдем эквивалентные сопротивления линий и трансформаторов:

По формуле (9.31) вычислим время наибольших потерь

Тогда по формуле (9.44) определим годовые потери электроэнергии
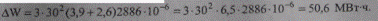
Полагая время использования наибольшей активной мощности равным времени использования наибольшей полной мощности ТНБ а = ТНБ = 4500 ч и принимая коэффициент мощности cosφ = 0,90, найдем годовую энергию, пропущенную через головной участок:
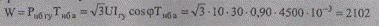
МВт-ч.
Потери энергии в процентах от переданной энергии составят:
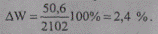
Зная эквивалентное сопротивление для данной сети, можно находить потери энергии при других токах головного участка в режиме наибольших нагрузок. Так, если ток головного участка увеличился в 2 раза, т. е. стал IГУ = 60 А, то потери энергии составят:

Переданная энергия

Потери энергии в процентах от переданной энергии
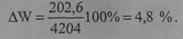
В общем виде потери электроэнергии в процентах от переданной энергии можно выразить так:
где 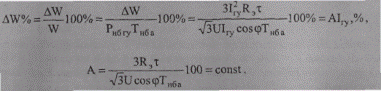
Следовательно, при неизменных параметрах сети (U, R3) и параметрах графика нагрузки (cosφ, ТНБ а) потери энергии в процентах пропорциональны току головного участка, что и подтвердил проведенный расчет. При увеличении тока в 2 раза с 30 А до 60 А потери энергии также увеличились в 2 раза с 2,4 % до 4,8 %.
Для вычисления потерь электроэнергии вероятностно-статистическим методом воспользуемся формулой (9.49), принимая в качестве магистрали линии 1 — 2 —4 — 7 — 9 (рис. 9.6):

что в процентах от переданной энергии составляет
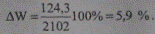
Найдем потери энергии в процентах по соответствующей формуле (9.51):
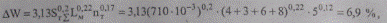
что несколько отличается от полученного значения по формуле (9.49).
Если в качестве расчетной модели принять формулу (9.50), то получим:
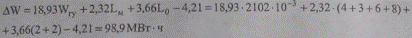
что в процентах от переданной энергии составляет
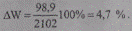
При вычислении потерь энергии в процентах по соответствующей формуле (9.52) получим:
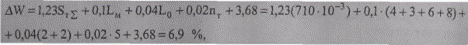
что близко к полученному по формуле (9.50) значению 6,8 %.
Из проведенных расчетов видно, что результаты по формулам (9.49) и (9.50) могут несколько отличаться. Отличаются они и от результата, полученного по методу эквивалентного сопротивления. Это объясняется тем, что по методу эквивалентного сопротивления вычисляются только нагрузочные потери, а по вероятностно-статистическому методу — как нагрузочные, так и потери холостого хода.
Расхождение в результатах по различным формулам может уменьшаться при увеличении в сети числа участков и трансформаторов.
ЗАДАЧА 9.3
Определить годовые потери электроэнергии в трехфазной сети напряжением 0,38 кВ длиной L = 0,30 км с симметричной нагрузкой по фазам (рис.9.8). Нагрузка равномерно распределена вдоль длины линии и в режиме наибольших нагрузок составляет р = 0,06 кВт/м с cosφ= 0,90. Линия выполнена маркой провода А 35. Время использования наибольшей нагрузки составляет ТНБ = 3000ч.

Рис. 9.8. Схема сети с равномерно распределенной нагрузкой Решение
Для марки провода А 35 удельные сопротивления равны r0 = 0,84 Ом/км и Хо = 0,31 Ом/км. Тогда сопротивления всей линии R = 0,84* 0,30 = 0,25 Ом, X= 0,31*0,30 = 0,09 Ом.
Ток, приходящийся на 1км линии,

а ток от всей заданной нагрузки Iнб = IНБ*L = 101,4-0,30 = 30,4 А.
Потери мощности в линии с распределенной нагрузкой равны потерям мощности от такой же сосредоточенной нагрузки, но подключенной на расстоянии 1/3 l от начала линии:

Потери мощности в процентах от передаваемой мощности

Время наибольших потерь определим по формуле (9.31):

Тогда потери электроэнергии по методу времени наибольших потерь

Переданная энергия (при ТНБа = ТНБ)
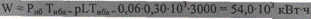
Потери энергии в процентах от переданной энергии
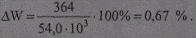
Определим теперь потери энергии через потери напряжения, которые для линии с распределенной нагрузкой равны потерям напряжения от такой же сосредоточенной нагрузки, но подключенной на расстоянии 1/2 от начала линии (см. параграф 9.9)
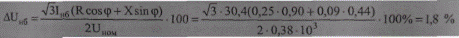
По формуле (9.57) найдем коэффициент перехода от потерь напряжения к потерям мощности:
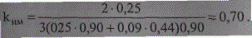
По формуле (9.55) определим потери мощности в процентах от передаваемой мощности:
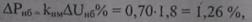
что практически соответствует найденным ранее потерям мощности.
Потери электроэнергии в процентах относительно переданной энергии по формуле(9.58)
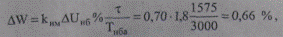
что практически соответствует найденным ранее потерям энергии.
Обратим внимание на то, что потери мощности в процентах от передаваемой мощности в режиме наибольших нагрузок оказываются больше потерь энергии в процентах от передаваемой энергии (ΔРНБ% > ΔW%).
ЗАДАЧА 9.4
Определить годовые потери электроэнергии в нерегулируемой батарее конденсаторов мощностью Q6K = 1000 квар, подключенной на шины 10 кВ подстанции. По условию работы предприятия, которое питается от этих шин, установлен следующий режим работы батареи конденсаторов: она отключается от сети на все выходные и праздничные дни и с 0 до 6 часов ежедневно в рабочие дни. Во все остальное время она работает с полной мощностью.
Решение
Определим время работы батареи конденсаторов, например, в 2005 году. Из 365 дней число выходных дней равно 52, а праздничных, не совпадающих с выходными, — 4, т. е. в течение полных суток батарея конденсаторов не будет работать 56 дней. Тогда количество рабочих дней составит 365 - 56 = 309, а количество рабочих часов Тбк = (24 - 6)309 = 5562 ч.
Годовые потери электроэнергии вычислим по формуле (9.61) при удельных потерях р = 0,002 кВт/квар;
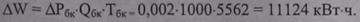
ЗАДАЧА 9.5
Определить годовые потери электроэнергии на корону в линии электропередачи длиной 200 км напряжением 330 кВ, выполненной с числом проводов в фазе, равном 2, площадью сечения каждого провода 400 мм2 и проходящей по территории Смоленской области. Построить зависимость изменения потерь электроэнергии на корону от среднеэксплуатационного напряжения в пределах от 0,95 до 1,UН0М.
Решение
Из табл. 9.2 для региона 1, соответствующего Смоленской области, находим удельные потери ΔWK та6л = 35,2 кВт-ч/(км*год). Тогда при длине линии L = 200 км получим

Потери электроэнергиипри реальном напряжении равны потерям, взятым из табл. 9.2 и умноженным на поправочный коэффициент kUk. Поэтому для построения зависимости изменения потерь на корону от напряжения достаточно вычислить этот коэффициент по формуле ( 9.7):

Задаваясь различным значением напряжения, получим:
Напряжение U/UНОМ 0 ,95 1,0 1,05 1,10
Коэффициент kUK 0,91 1,0 1,41 1,83
Результаты представлены на рис.9.9. Из результатов расчета видно, что потери мощности и энергии на корону сильно зависят от напряжения. При повышении напряжения на 10% относительно номинального они увеличиваются в 1,83 раза.
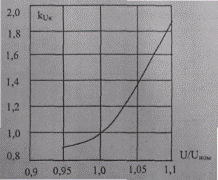
Рис. 9.9. Зависимость kUK от напряжения
ЗАДАЧА 9.6
Определить потери электроэнергии за сутки в воздушной линии электропередачи длиной 30 км, выполненной маркой провода АС 120/19, если в течение 12 ч при температуре окружающего воздуха tB = 0 по ней пропускается ток I = 200 А, а в течение остальных 12 ч суток при температуре tB=20°С — предельно допустимый ток I = 380 А.
Решение
Для решения задачи воспользуемся формулой (9.9), по которой вычисляется активное сопротивление провода:
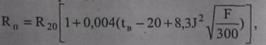
где F- площадь сечения провода; J — плотность тока, равная J = I/F.
Для заданной марки провода при tB =20°С из справочников найдем активное сопротивление R20=0,27 Ом/км. Тогда при tB= 0 получим:
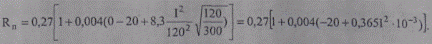
Подставляя различные значения тока, найдем сопротивление провода, соответствующее данному току при tB=0. Так, при токе I = 200 А получим:

Аналогичным образом при tВ = 20°С получим:
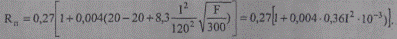
Результаты расчетов при различных значениях тока приведены в табл. 9.6.
Таблица 9.6
Активные сопротивления провода при различном токе
| Температура воздуха tB,°C | Параметры | Ток,А | ||||
| RП, Ом/км | 0,248 | 0,252 | 0,264 | 0,284 | 0,306 | |
| RП/R20 | 0,92 | 0,934 | 0,979 | 1,051 | 1,135 | |
| RП, Ом/км | 0,27 | 0,274 | 0,286 | 0,310 | 0,330 | |
| RП/R20 | 1,014 | 1,059 | 1,131 | 1,215 |
Из табл. 9.6 видны изменения активного сопротивления провода в зависимости от температуры провода и пропускаемого тока. Так, при tВ =20 С и токе I = 380 А сопротивление провода по сравнению с током I = 0 увеличивается в 1,215 раза.
Найдем теперь потери электроэнергии в соответствии с заданным режимом работы линии:
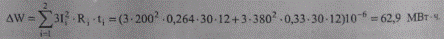
Определим также потери энергии без учета зависимости активного сопротивления от температуры воздуха и тока линии

Погрешность расчета составляет
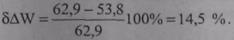
Дата добавления: 2021-02-19; просмотров: 689;











