Непрерывные проценты

В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при обосновании и выборе инвестиционных решений.

Наращенная сумма при дискретных процентах определяется по формуле

S=P(1+j/m)^mn,

где j – номинальная ставка процентов, а m – число периодов начисления процентов в году.

Чем больше m, тем меньше промежутки времени между моментами начисления процентов. Увеличение частоты начисления процентов (m) при фиксированном значении номинальной процентной ставки j приводит к росту множителя наращения, который при непрерывном начислении процентов (m®¥) достигает своего предельного значения

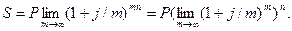(2.5)

Известно, что

,

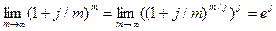где е – основание натуральных логарифмов.

Используя этот предел в выражении (2.5), окончательно получаем, что наращенная сумма по ставке j равна

S=Pe^jn.

Непрерывную ставку процентов называют силой роста и обозначают символом d. Тогда

S=Pe^dn. (2.6)

Сила роста d представляет собой номинальную ставку процентов при m®¥.

Закон наращения при непрерывном начислении процентов (2.6) совпадает по форме с (2.2) с той разницей, что в (2.2) время изменяется дискретно с шагом 1/m, а в (2.6) – непрерывно.

Легко показать, что дискретные и непрерывные ставки наращения находятся в функциональной зависимости. Из равенства множителей наращения можно получить формулу эквивалентного перехода от одних ставок к другим:

(1+i)ⁿ=e^dn,

откуда следует:

d=ln(1+i), i=e^d-1.

Пример 20. Сумма, на которую начисляются непрерывные проценты в течение 5 лет, равна 2000 ден. ед., сила роста 10%. Наращенная сумма составит S=2000·e^0,1·5=2000·1,6487=3297,44 ден. ед.

Непрерывное наращение по ставке 10% равнозначно наращению за тот же срок сложных дискретных процентов по годовой ставке i. Находим:

i=e^0,1-1=1,10517-1=0,10517.

В итоге получим S=2000·(1+0,10517)⁵=3297,44 ден. ед.

Дисконтирование на основе силы роста осуществляется по формуле

P=Se^-dn

Пример 21. Определим современную стоимость платежа из примера 17 при условии, что дисконтирование производится по силе роста 15%.

Решение. Полученная за долг сумма (современная величина) равна

P=5000·е^-0,15·5=5000·0,472366=2361,83 ден. ед.

При применении дискретной сложной учетной ставки такого же размера получили величину (см. пример 17) P=2218,53 ден. ед.