Лекция 7. Непрерывные методы модуляции и манипуляции
Методы модуляции
При передаче информации по непрерывному каналу используется определенный физический процесс, называемый переносчиком или несущей.
Математической моделью переносчика может служить функция времени l(t,A,B,…), зависящая также от параметров А, В,….
Некоторые параметры функции фиксированы при данных условиях передачи, и тогда они могут исполнять роль идентифицирующих параметров, т.е. по ним можно определять принадлежность данного сигнала к определенному классу сигналов.
Другие параметры подвергаются воздействию со стороны передатчика. Это воздействие на них называется модуляцией, а эти параметры исполняют роль информативных параметров.
В общем случае модуляция есть отображение множества возможных значений входного сигнала на множество значений информативного параметра переносчика. Устройство, осуществляющее модуляцию, называется модулятором. На один вход модулятора действует реализация входного сигнала x(t), на другой– сигнал- переносчик l(t,A). Модулятор формирует выходной сигнал l(t,A[x(t)]), информативный параметр которого изменяется во времени в соответствии с передаваемым сигналом. В более узком смысле под модуляцией понимается воздействие на переносчик, выражающееся в умножении информативного, т.е. модулируемого параметра на множитель [1+M*h(t)], где h(t)- модулирующая функция, соответствующая реализации x(t) входного сигнала, определяемая так, что ½h(t)½£1, а М – коэффициент модуляции.
Основное назначение модуляции состоит в перенесении спектра сигнала в заданную частотную область для обеспечения возможности передачи его по каналу и повышения помехоустойчивости передачи.
В зависимости от вида используемого при модуляции переносчика различают непрерывные и импульсные виды модуляции. При непрерывной модуляции в качестве несущего используется гармоническое колебание. При импульсной модуляции в качестве несущей используется периодическая последовательность прямоугольных импульсов.
Рассмотрим основные принципы непрерывных методов модуляции, когда в качестве переносчика или несущей или модулируемого напряжения используется гармоническое напряжение 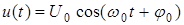 , где
, где 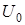 -амплитуда напряжения,
-амплитуда напряжения, 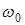 -несущая частота,
-несущая частота, 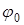 -начальная фаза (рис. 2.7).
-начальная фаза (рис. 2.7).
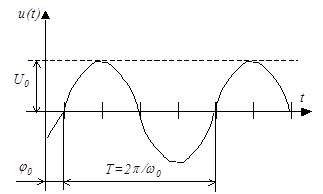
| 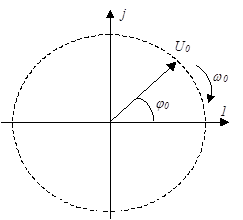
|
| Рисунок 2.7. Гармоническое напряжение | Рисунок 2.8. Гармоническое напряжение |
Это напряжение можно представить на комплексной плоскости в виде вектора длиной 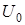 (рис. 2.8). Этот вектор в начальный момент времени t=0 повернут к вещественной оси на угол
(рис. 2.8). Этот вектор в начальный момент времени t=0 повернут к вещественной оси на угол 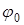 и вращается со скоростью
и вращается со скоростью 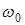 , т.е. в любой другой момент времени повернут на угол
, т.е. в любой другой момент времени повернут на угол 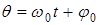 . Его проекция
. Его проекция 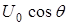 на вещественную ось в любой момент времени равна мгновенному значению напряжения
на вещественную ось в любой момент времени равна мгновенному значению напряжения 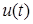 .
.
При модуляции 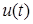 первичными сигналами или модулирующим напряжением можно воздействовать на амплитуду (амплитудная модуляция), частоту (частотная модуляция) или фазу (фазовая модуляция).
первичными сигналами или модулирующим напряжением можно воздействовать на амплитуду (амплитудная модуляция), частоту (частотная модуляция) или фазу (фазовая модуляция).
При этом следует заметить, что аргумент гармонического колебания 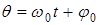 , называемый полной фазой, определяет текущее значение фазового угла, в связи с чем ЧМ и ФМ получили обобщающее название угловой модуляции.
, называемый полной фазой, определяет текущее значение фазового угла, в связи с чем ЧМ и ФМ получили обобщающее название угловой модуляции.
В случае амплитудной модуляции (АМ) частота модулируемого напряжения не изменяется и остается равной 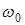 , начальная фаза
, начальная фаза 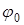 задается моментом начала модуляции, а амплитуда изменяется в соответствии с законом изменения величины модулирующего напряжения (рис. 2.9).
задается моментом начала модуляции, а амплитуда изменяется в соответствии с законом изменения величины модулирующего напряжения (рис. 2.9).
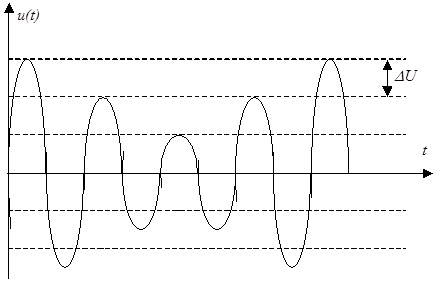
|
| Рисунок 2.9. Гармоническое напряжение, модулированное по амплитуде |
Если обозначить 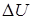 - наибольшее изменение амплитуды модулированного напряжения, то амплитуда модулированного напряжения может быть определена как
- наибольшее изменение амплитуды модулированного напряжения, то амплитуда модулированного напряжения может быть определена как
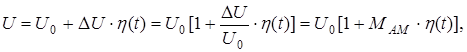
|
где h(t)-закон изменения модулирующего напряжения, а 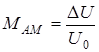 – относительное изменение амплитуды, которое называется коэффициентом или глубиной АМ.
– относительное изменение амплитуды, которое называется коэффициентом или глубиной АМ.
Таким образом, напряжение, модулированное по амплитуде, можно записать как
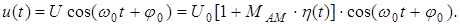
|
Рассмотрение спектра сигнала, модулированного по амплитуде, целесообразно начать с простейшего случая, когда модулирующий сигнал- простое гармоническое колебание 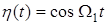 , имеющее наиболее простой спектр – одну спектральную линию.
, имеющее наиболее простой спектр – одну спектральную линию.
Положив 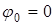 , получим
, получим
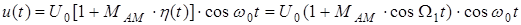 . .
|
После несложных преобразований можно получить
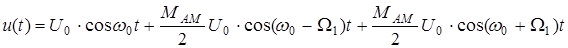
|
Таким образом, в этом случае спектр сигнала, модулированного по амплитуде, состоит из трех гармонических составляющих (рис. 2.10): несущей с частотой 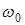 и двух боковых – нижней с частотой
и двух боковых – нижней с частотой 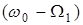 и верхней с частотой
и верхней с частотой 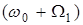 .
.
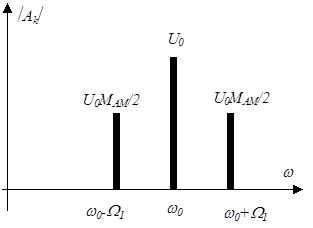
|
| Рисунок 2.10. Спектр сигнала, модулированного по амплитуде |
В общем случае, когда спектр модулирующего сигнала представляет собой не одну спектральную линию, а полосу частот от 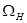 до
до 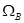 , для получения спектра модулированного колебания нужно: 1) сместить спектр модулирующего сигнала на интервал частот, равный несущей; 2) построить зеркальное отображение смещенного спектра относительно спектральной линии на несущей частоте
, для получения спектра модулированного колебания нужно: 1) сместить спектр модулирующего сигнала на интервал частот, равный несущей; 2) построить зеркальное отображение смещенного спектра относительно спектральной линии на несущей частоте 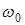 (рис. 2.11).
(рис. 2.11).
Таким образом, полоса частот напряжения, модулированного по амплитуде, зависит от максимальной частоты модулирующего сигнала 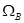 и равна
и равна 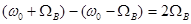 , т.е. вдвое больше максимальной частоты спектра модулирующего сигнала.
, т.е. вдвое больше максимальной частоты спектра модулирующего сигнала.
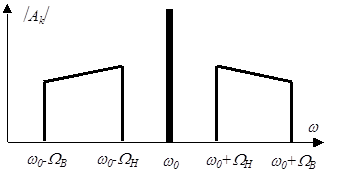
|
| Рисунок 2.11. Спектр сигнала, модулированного по амплитуде |
Если первичный модулирующий сигнала представляет собой последовательность однополярных или двуполярных прямоугольных импульсов, что и имеет место на входе дискретного канала, то такой вид модуляции называется манипуляцией. При амплитудной манипуляции модулированный сигнал представляет собой гармоническое колебание с частотой несущей, амплитуда которого в общем случае принимает лишь два значения: 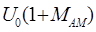 и
и 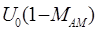 . Если спектр модулирующего колебания известен, то можно построить спектр сигнала после амплитудной манипуляции по общему правилу: сместить спектр модулирующего сигнала в область несущей и зеркально отобразить его относительно несущей.
. Если спектр модулирующего колебания известен, то можно построить спектр сигнала после амплитудной манипуляции по общему правилу: сместить спектр модулирующего сигнала в область несущей и зеркально отобразить его относительно несущей.
Пусть, например, модулирующий сигнал – последовательность прямоугольных импульсов со скважностью, равной двум. Спектр такого сигнала, как известно, бесконечен и содержит постоянную составляющую (для однополярных импульсов) и бесконечное число нечетных гармоник, т.к. амплитуды гармоник, номера которых кратны скважности, равны нулю (рис. 2.12).
Если спектр модулирующего сигнала ограничить с помощью ФНЧ частотой 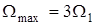 , то ширина спектра манипулированного сигнала составит
, то ширина спектра манипулированного сигнала составит 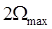 =6W1.Спектр сигнала можно ограничить и после манипуляции с помощью полосового фильтра с полосой пропускания
=6W1.Спектр сигнала можно ограничить и после манипуляции с помощью полосового фильтра с полосой пропускания 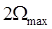 .
.
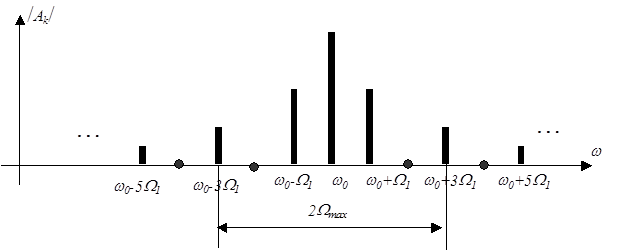
|
| Рисунок 2.12. Спектр сигнала, манипулированного по амплитуде |
Ограничение полосы приводит к искажению прямоугольной формы огибающей модулированного сигнала, а следовательно и к искажению формы восстановленного после демодуляции первичного сигнала. Однако для практики часто оказывается достаточно передать первую и третью гармоники сигнала, т.к. при этом сохраняется более 90% энергии исходного сигнала.
Передача АМ-сигнала с указанным спектром получила название метода передачи двух боковых и несущей. Основным достоинством этого метода является относительная простота модулятора и демодулятора и канальных фильтров.
Один из основных недостатков состоит в удвоении требуемой полосы частот по сравнению с полосой частот исходного сигнала. Другой недостаток вытекает из соотношения мощностей несущей и боковых. Можно доказать, что 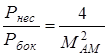 , т.е. например, при МАМ=0,2 мощность несущей в 100 раз превосходит мощность боковых. Следовательно, при формировании канального сигнала по этому методу уровень сигнала, на который накладываются жесткие ограничения сверху, вызванные, во-первых, необходимостью уменьшения влияний на другие каналы и, во-вторых, необходимостью исключения перегрузки канальных усилителей, определяется в основном мощностью несущей, не содержащей информации о модулирующем сигнале, которая содержится в боковых.
, т.е. например, при МАМ=0,2 мощность несущей в 100 раз превосходит мощность боковых. Следовательно, при формировании канального сигнала по этому методу уровень сигнала, на который накладываются жесткие ограничения сверху, вызванные, во-первых, необходимостью уменьшения влияний на другие каналы и, во-вторых, необходимостью исключения перегрузки канальных усилителей, определяется в основном мощностью несущей, не содержащей информации о модулирующем сигнале, которая содержится в боковых.
С учетом этих недостатков используется метод передачи одной боковой полосы (АМ-ОБП), который свободен от них. Кроме того, подавление несущей дает возможность при заданных ограничениях на уровень канального сигнала увеличить мощность боковой и, тем самым, повысить помехозащищенность сигнала.
Устранение несущей осуществляется использованием специальных балансных модуляторов. Подавление одной из боковых полос осуществляется различными методами. Простейшим из них является использование соответствующих полосовых фильтров, к которым, однако, предъявляются достаточно высокие требования по крутизне спадов АЧХ и величине затухания в полосе непропускания. Эти требования, а следовательно и трудность реализации фильтра, возрастают с ростом частоты несущей. Другим методом является т.н. фазоразностный метод. Его суть состоит в использовании двух модуляторов, на один из которых подаются исходный сигнал и несущая, а на другой – они же, но сдвинутые по фазе на 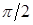 . На выходе схемы, который представляет собой объединение выходов этих модуляторов через развязывающее устройство, сигнал будет содержать колебания только одной боковой полосы.
. На выходе схемы, который представляет собой объединение выходов этих модуляторов через развязывающее устройство, сигнал будет содержать колебания только одной боковой полосы.
Существенным недостатком АМ-ОБП является то, что на приеме колебания несущей должны быть восстановлены от местного генератора при достаточно строгом соблюдении синхронности. Если на приеме восстановлена частота несущей 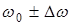 , где
, где 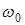 - частота несущей на передаче, то это приведет к смещению спектра восстановленного первичного сигнала на величину
- частота несущей на передаче, то это приведет к смещению спектра восстановленного первичного сигнала на величину 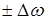 . Это смещение, в свою очередь, приводит к появлению амплитудно-частотных искажений, которые могут привести к возникновению ошибок в принятом сообщении.
. Это смещение, в свою очередь, приводит к появлению амплитудно-частотных искажений, которые могут привести к возникновению ошибок в принятом сообщении.
При частотной модуляции амплитуда модулируемого напряжения остается постоянной, а частота меняется в соответствии с законом изменения модулирующего колебания. Такое напряжение можно представить на комплексной плоскости вектором постоянной длины, который вращается с изменяющейся скоростью. Мгновенное значение модулированного напряжения есть проекция этого вектора на вещественную ось, т.е. 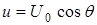 , где q- угол между вектором U0 и вещественной осью. Так как по определению мгновенная угловая скорость вращения вектора
, где q- угол между вектором U0 и вещественной осью. Так как по определению мгновенная угловая скорость вращения вектора 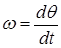 , то
, то 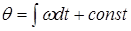 . Постоянная интегрирования определяет положение вектора в начальный момент времени, следовательно
. Постоянная интегрирования определяет положение вектора в начальный момент времени, следовательно 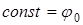 . Тогда
. Тогда 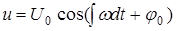 .
.
Если частота w при частотной модуляции может меняться относительно некоторой частоты w0 в некоторых пределах, тогда 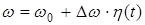 , где
, где 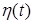 - закон изменения модулирующего сигнала, а
- закон изменения модулирующего сигнала, а 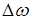 называется девиацией частоты. Тогда можно записать
называется девиацией частоты. Тогда можно записать
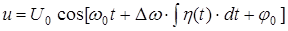 . .
|
Для нахождения спектра ЧМ- сигнала положим 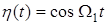 и
и 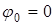 .
.
Тогда
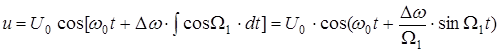 , ,
|
где 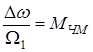 называется индексом частотной модуляции.
называется индексом частотной модуляции.
Последнее выражение может быть преобразовано
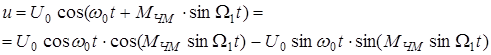
|
Функции 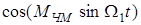 и
и 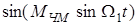 раскладываются в ряды, но не тригонометрических функций, а функций Бесселя первого рода J(MЧМ) соответственно четного J2k(МЧМ) и нечетного J2k+1(МЧМ) порядков, т.е.
раскладываются в ряды, но не тригонометрических функций, а функций Бесселя первого рода J(MЧМ) соответственно четного J2k(МЧМ) и нечетного J2k+1(МЧМ) порядков, т.е.
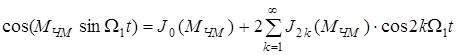
|
и
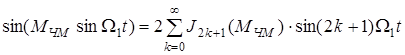
|
После подстановок и преобразований получим
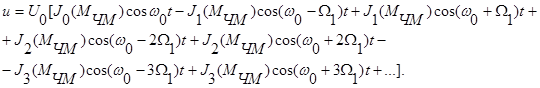
|
Таким образом, спектр ЧМ-сигнала при гармонической несущей и гармоническом модулирующем сигнале состоит из колебания на несущей частоте w0, амплитуда которого пропорциональна бесселевой функции нулевого порядка и бесконечного числа верхних и нижних боковых с частотами w0+kW1, амплитуды которых пропорциональны бесселевым функциям соответствующих порядков.
Если в качестве модулирующего напряжения используется последовательность прямоугольных импульсов, то такая частотная модуляция называется частотной манипуляцией. Если частотная манипуляция осуществляется без разрыва фазы несущей, то, рассматривая простейший случай, когда скважность модулирующих импульсов равна двум, можно из приведенных ранее выражений получить формулы для амплитуд спектральных составляющих:
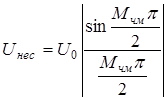 , ,
|
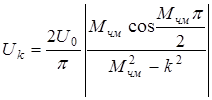 для нечетных k, для нечетных k,
|
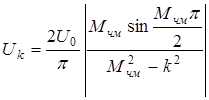 для четных k, для четных k,
|
где k- номер гармоники с частотой 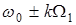 ,
, 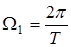 , T- период модулирующих импульсов. Поскольку спектр теоретически бесконечен, то возникает вопрос о практически необходимой ширине спектра, т.е. о том, сколько нужно передавать гармоник, чтобы передать более 90% энергии сигнала.
, T- период модулирующих импульсов. Поскольку спектр теоретически бесконечен, то возникает вопрос о практически необходимой ширине спектра, т.е. о том, сколько нужно передавать гармоник, чтобы передать более 90% энергии сигнала.
Из приведенных формул видно, что амплитуды спектральных составляющих зависят от МЧМ – индекса частотной модуляции (рис. 2.13).

|
| Рисунок 2.13. Спектры сигналов при частотной модуляции |
Чем меньше индекс частотной модуляции, тем меньшее число боковых составляющих нужно принимать во внимание и тем уже практически необходимая ширина спектра ЧМ-сигнала.
Поэтому частотную модуляцию при МЧМ<1 называют узкополосной. В этом случае ширина спектра 2W1, а его вид почти такой же, как и при АМ, отличаясь от него лишь значениями амплитуд спектральных составляющих. Число n сохраняемых боковых при МЧМ > 1 рекомендуется определять как n=МЧМ+1, тогда необходимая ширина спектра 2W1 n = 2W1(МЧМ+1 = 2(Dw+W1).
При больших индексах частотной модуляции МЧМ >> 1 можно пренебречь 1 по сравнению с МЧМ и тогда 2W1 n = 2W1МЧМ = 2Dw, т.е. необходимая ширина спектра равна удвоенной величине девиации частоты и не зависит от частоты W1 модулирующего сигнала. Частотную модуляцию при МЧМ>>1 называют широкополосной, так как при больших индексах модуляции удельный вес боковых составляющих высоких номеров k растет. Этот рост продолжается пока k, увеличиваясь, приближается к МЧМ, а затем при k>МЧМ быстро убывает, поэтому можно ограничить спектр гармониками с k=МЧМ. Основное преимущество широкополосной ЧМ – значительно большая помехоустойчивость, чем АМ и узкополосной ЧМ.
При фазовой модуляции в соответствии с законом изменения модулирующего сигнала, так же как и при частотной модуляции, изменяется полная фаза q. Но если при частотной модуляции
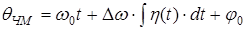 , ,
|
то при фазовой модуляции
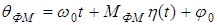 , ,
|
где МФМ представляет собой максимальное значение фазового сдвига и называется индексом фазовой модуляции.
Тогда мгновенное значение напряжения, модулированного по фазе, может быть записано как
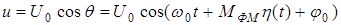 .
.
Таким образом принципиальное отличие ЧМ и ФМ состоит в том, что при ФМ фазовый сдвиг между ФМ-сигналом и немодулированным колебанием пропорционален h(t), а при ЧМ фазовый сдвиг между ЧМ-сигналом и немодулированным колебанием пропорционален интегралу от h(t).
Спектр ФМ-сигнала при гармоническом модулирующем сигнале 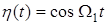 по виду получается таким же как и при ЧМ. Действительно, если записать
по виду получается таким же как и при ЧМ. Действительно, если записать
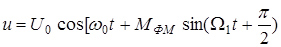
и сопоставить с аналогичным выражением для ЧМ, то это будет очевидным. Однако следует иметь в виду, что ЧМ и ФМ- сигналы ведут себя по разному при изменении частоты и амплитуды модулирующего напряжения. Это объясняется тем, что индекс фазовой модуляции МФМ = Djm= KUW, где К – коэффициент пропорциональности, UW - амплитуда модулирующего сигнала.
Таким образом, индекс фазовой модуляции пропорционален амплитуде модулирующего сигнала и не зависит от его частоты, в то время как индекс частотной модуляции в общем случае зависит как от амплитуды, поскольку от нее зависит девиация частоты, так и от частоты модулирующего сигнала.
В простейшем случае фазовой манипуляции гармонической несущей используется изменение фазы несущей на 1800 (рис. 2.14). Такой сигнал можно представить как сумму сигнала, модулированного по амплитуде, с удвоенной амплитудой и несущей в противофазе. В связи с этим вид спектра сигнала, манипулированного по фазе, практически совпадает с видом спектра сигнала, манипулированного по амплитуде.
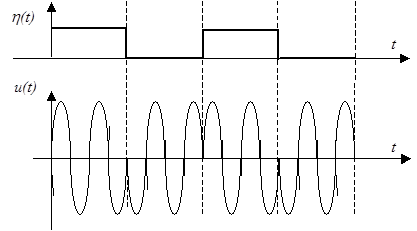
|
| Рисунок 2.14. Фазовая манипуляция |
При фазовой манипуляции с МФМ=1800 амплитуды несущей и боковых могут быть рассчитаны по формулам
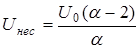 ,
,
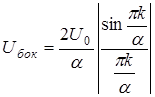 ,
,
где k- номер боковой гармоники, a- скважность модулирующего сигнала. Таким образом, при a=2 в спектре сигнала, манипулированного по фазе, отсутствует несущая. Практически необходимая ширина спектра при ФМ такая же, как и при ЧМ.
Рассмотренные вопросы исследуются в лабораторной работе №5 «Спектры манипулированных сигналов» [1. с. 51-61].
Основной технической проблемой, возникающей при реализации такого метода фазовой манипуляции, является создание в месте приема синфазного с сигналом опорного немодулированного напряжения (несущей), путем сравнения фазы которого с фазой принимаемого ФМ-сигнала в фазовом детекторе осуществляется демодуляция. Поскольку почти во всех реальных каналах фаза напряжения принимаемого сигнала флуктуирует, то решение этой проблемы путем создания высокостабильного местного генератора опорного напряжения исключается в принципе. Влияние флуктуации фазы сигнала на достоверность приема может быть значительно ослаблено, если формировать опорное напряжение (несущую) из самого принимаемого сигнала. Существуют различные схемы формирования опорного напряжения, однако практически для всех из них характерно явление, называемое обратной работой, и состоящее в том, что под действием на передаваемый сигнал помех возможно скачкообразное изменение фазы формируемого на приемной стороне опорного напряжения на 1800. Это вызовет изменение полярности посылок на выходе демодулятора, т.е. «1» будут регистрироваться как «0» и наоборот. Искажается вся дальнейшая последовательность принимаемых элементов.
От явления обратной работы свободен метод относительной фазовой модуляции (ОФМ), который отличается от ФМ тем, что при передаче «1» фаза несущего колебания передаваемого элемента остается той же, что и у предыдущего элемента вне зависимости от того, каким был предыдущий элемент (0 или 1), а при передаче «0» его фаза меняется на 1800 вне зависимости от того, каким был предыдущий элемент (0 или 1) (рис. 2.15).
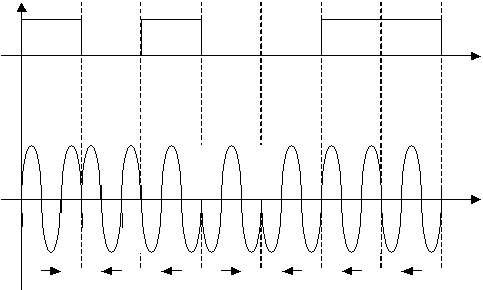
|
| Рисунок 2.15. Относительная фазовая манипуляция |
На приемной стороне для выявления информации (0 или 1), заключенной в каждом данном элементе, он сопоставляется (сравнивается по фазе) с предыдущим элементом. Если фаза не изменилась, регистрируется 1, если изменилась – 0. Практически необходимая ширина спектра при ОФМ такая же, как и при ФМ.
Если в качестве манипулирующего элемента в ОФМ используется не один бит, а совокупность из N бит, то имеет место т.н. многократная или N- кратная ОФМ. Принцип многократной ОФМ заключается в том, что каждой последовательности из N бит присваивается определенное значение фазового угла несущего колебания. Следовательно, для N- кратной ОФМ необходимо использовать 2N различных значений фазовых сдвигов несущего колебания, кратных некоторому минимальному углу манипуляции, равному Djmin=2p/2N.
При двукратной ОФМ (ДОФМ) Djmin=p/2 и используются два варианта (табл. 2.1) наборов фаз в зависимости от манипуляционного элемента, называемого в этом случае дибитом.
| Таблица 2.1. Варианты ДОФМ | ||
| дибит | 1 вариант | 2 вариант |
| 00 | 450 | |
| 900 | 1350 | |
| 2700 | 3150 | |
| 1800 | 2250 |
Таким образом, при ДОФМ передаваемый сигнал имеет четыре возможных значения фазы, однако, как и в случае ОФМ, информация содержится в соотношении фаз соседних элементов. При трехкратной ОФМ (ТОФМ) Djmin=p/4, а манипуляционный элемент представляет собой совокупность из трех бит, называемую трибитом.
В каждой конкретной системе, использующей многократную ОФМ, манипуляционный элемент (дибит или трибит), может быть образован по разному. Это, во-первых, могут быть смежные элементы одной информационной последовательности. Тогда за счет использования многократной ОФМ обеспечивается увеличение удельной скорости передачи по каналу. Во-вторых, каждый из разрядов дибита или трибита можно рассматривать как элементы различных независимо формируемых информационных последовательностей. Это означает, что в полосе частот канала организуется два или три канала, что называется вторичным уплотнением. Наконец, в-третьих, дибит или трибит может быть получен с выхода кодера сверточного кодера, если не коммутировать выходы сумматоров по модулю два, а подавать их непосредственно на входы модулятора многократной ОФМ.
Помехоустойчивость систем с относительной фазовой манипуляцией резко уменьшается по мере увеличения кратности, что главным образом обусловлено воздействием флуктуационных помех. Однако, во многих реальных каналах помехоустойчивость в основном определяется действием импульсных помех, а флуктуационные играют второстепенную роль.
Поэтому в проводных каналах связи системы с ДОФМ и ТОФМ находят достаточно широкое применение, обеспечивая существенное увеличение скорости передачи при незначительном снижении достоверности.
Системы с относительной фазовой манипуляцией при кратности более трех используются редко из-за сложности реализации и низкой помехоустойчивости.
Большее применение находят многопозиционные системы с одновременной амплитудной и фазовой манипуляцией при однополосной передаче. В наиболее общем виде этот принцип выражен в т.н. квадратурной амплитудной модуляции (КАМ). Квадратурное представление сигналов является удобным и достаточно универсальным средством их описания. Квадратурное представление заключается в выражении колебания линейной комбинацией двух ортогональных составляющих – синусоидальной и косинусоидальной: 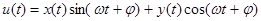 , где x(t) и y(t) – дискретные величины, представляющие собой входные манипулирующие воздействия, которые могут быть как биполярными, так и многоуровневыми. Такая манипуляция осуществляется по двум каналам на несущих, сдвинутых друг относительно друга на 900, т.е. находящихся в квадратуре, откуда и первое слово в названии метода модуляции. Поскольку для него характерна взаимная независимость многоуровневых манипулирующих импульсов x(t) и y(t), то выходной сигнал u(t) квадратурной схемы изменяется не только по фазе, но и по амплитуде, откуда второе слово в названии метода модуляции.
, где x(t) и y(t) – дискретные величины, представляющие собой входные манипулирующие воздействия, которые могут быть как биполярными, так и многоуровневыми. Такая манипуляция осуществляется по двум каналам на несущих, сдвинутых друг относительно друга на 900, т.е. находящихся в квадратуре, откуда и первое слово в названии метода модуляции. Поскольку для него характерна взаимная независимость многоуровневых манипулирующих импульсов x(t) и y(t), то выходной сигнал u(t) квадратурной схемы изменяется не только по фазе, но и по амплитуде, откуда второе слово в названии метода модуляции.
Любые сигналы, пользуясь геометрической интерпретацией, можно изобразить векторами в сигнальном пространстве. Отмечая только концы векторов, получим совокупность точек, которая называется сигнальным созвездием.
Сигнальное созвездие для случая, когда x(t) и y(t) принимают значения + 1 и + 3 (т.н. четырехуровневая КАМ) приведена на рис. 2.16. Величины + 1 и + 3 определяют уровни модуляции и имеют относительный характер. Созвездие содержит 16 сигнальных точек (КАМ-16), каждая из которых соответствует четырем передаваемым информационным битам.
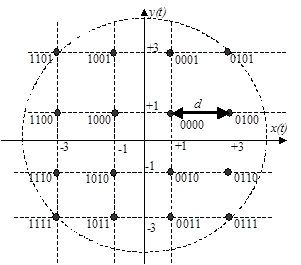
| 
|
| Рисунок 2.16. Сигнальное созвездие КАМ | Рисунок 2.17. Сигнальное созвездие ОФМ |
Из теории связи известно, что при равном числе точек в сигнальном созвездии спектр сигналов КАМ идентичен спектру сигналов ОФМ. Однако помехоустойчивость систем ОФМ и КАМ различна. Сравнение ансамблей сигнальных точек по помехоустойчивости удобно производить по коэффициенту помехоустойчивости, в котором соотносятся минимальное расстояние между сигнальными точками и энергетические затраты на передачу одного бита.
Расстояние между сигнальными точками в системе с ОФМ (рис. 2.17) определяется по формуле 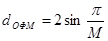 , где М- число фазовых углов.
, где М- число фазовых углов.
Расстояние между сигнальными точками в системе КАМ с L уровнями манипулирующих импульсов определяется по формуле
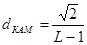 .
.
Например, когда М=16, а следовательно L=4, 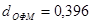 , а
, а 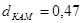 при одном и том же уровне мощности. Это говорит о том, что данная система с КАМ предпочтительнее данной системы с ОФМ по помехоустойчивости.
при одном и том же уровне мощности. Это говорит о том, что данная система с КАМ предпочтительнее данной системы с ОФМ по помехоустойчивости.
Рассмотренные вопросы исследуются в лабораторной работе №6 «Помехоустойчивость приема единичных элементов при различных видах модуляции» [1. c. 62-69].
Контрольные вопросы к лекции 7
7-1. Что служит математической моделью несущей при модуляции?
7-2. Для чего служат идентифицирующие параметры несущей?
7-3. Для чего служат информативные параметры несущей?
7-4. Какой процесс называется модуляцией?
7-5. В чем состоит основное назначение модуляции?
7-6. Какие методы модуляции называются непрерывными?
7-7. Какие методы модуляции называются угловой модуляцией?
7-8. Что называется коэффициентом или глубиной амплитудной модуляции?
7-9. Какие составляющие содержит спектр сигнала при амплитудной модуляции гармонической несущей гармоническим модулирующим сигналом?
7-10. От чего зависит амплитуда боковых при амплитудной модуляции гармонической несущей гармоническим модулирующим сигналом?
7-11. Каким образом можно построит спектр модулированного сигнала при амплитудной модуляции гармонической несущей произвольным модулирующим сигналом с известным спектром?
7-12. Чему равна полоса частот напряжения, модулированного по амплитуде?
7-13. Какой вид модуляции называется манипуляцией?
7-14. Почему при амплитудной манипуляции следует говорить лишь о практически необходимой ширине спектра манипулированного сигнала?
7-15. В чем состоят недостатки использования для передачи АМ-сигнала с двумя боковыми?
7-16. Какое преимущество обеспечивает применение АМ-ОБП?
7-17. Какое преимущество обеспечивает подавление несущей при передаче АМ-сигнала?
7-18. В чем состоит недостаток применения АМ-ОБП с подавлением несущей?
7-19. Что называется девиацией частоты при частотной модуляции?
7-20. Что называется индексом частотной модуляции?
7-21. Какова теоретическая ширина спектра ЧМ-сигнала?
7-22. Как практически необходимая ширина спектра ЧМ-сигнала зависит от индекса частотной модуляции?
7-23. Какую частотную модуляцию называют узкополосной?
7-24. Какую частотную модуляцию называют широкополосной?
7-25. Чему равна практически необходимая ширина спектра при широкополосной частотной модуляции?
7-26. В чем состоит основное преимущество широкополосной ЧМ?
7-27. Что называется индексом фазовой модуляции?
7-28. В чем состоит принципиальное отличие ЧМ и ФМ?
7-30. От чего зависит индекс фазовой модуляции?
7-31. Как выглядит спектр сигнала манипулированного по фазе?
7-32. Какое явление называется обратной работой?
7-33. Чем ОФМ отличается от ФМ?
7-34. Какая ОФМ называется многократной?
7-35. Как может быть образован манипуляционный элемент при использовании ДОФМ или ТОФМ?
7-36. В чем состоят преимущества применения ДОФМ или ТОФМ?
7-37. Какие параметры несущей манипулируются при использовании КАМ?
7-38. Что называется сигнальным созвездием?
7-39. Сколько бит содержит манипуляционный элемент при использовании КАМ-16?
7-40. Как с помощью сигнальных созвездий можно сравнивать различные виды модуляции по помехоустойчивости?
Дата добавления: 2020-10-14; просмотров: 810;











