Эквивалентность процентных ставок.
Как было показано выше, для процедур наращения и дисконтирования могут применяться ставки процентов различного типа: простые и сложные процентные и учетные ставки. В связи с тем, что контракты могут быть составлены с использованием различных видов ставок, то для сопоставления их доходности возникает необходимость в установлении правил эквивалентного приведения различных ставок к ставке одного вида. Динамика процессов наращения и дисконтирования определяется только временнóй зависимостью множителя наращения и дисконтного множителя и не зависит от величины первоначальной и конечной сумм. Поэтому замена одного типа ставки на другой не изменит отношения сторон в рамках конкретного контракта, если от такой замены соответствующие множители не изменятся. Такие ставки называют эквивалентными. Проблема эквивалентности ставок уже затрагивалась в п. 2.2. при определении эффективной ставки процента. В принципе соотношение эквивалентности можно найти для любой пары различного вида ставок – простых и сложных, дискретных и непрерывных.
Формулы эквивалентности ставок во всех случаях выводятся из равенства взятых попарно множителей наращения. Например, для определения соотношения эквивалентности между простой и сложной ставками приравняем соответствующие множители наращения:
(1+nis)=(1+i)n,
где is и i – ставки простых и сложных процентов. Решение равенства дает следующие соотношения эквивалентности:
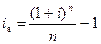 ;
;
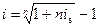 .
.
Соотношения между численными значениями двух эквивалентных друг другу различных типов ставок зависит от срока контракта: ставки, эквивалентные при одном сроке контракта, неэквивалентны при другом его значении.
Пример 25. Необходимо найти величину простой учетной ставки (К=360), эквивалентной годовой простой процентной ставке 40% (К=365) при условии, что срок учета равен 255 дням.
Решение. Для установления эквивалентности воспользуемся исходными формулами S = P (1+ni) и P = S (1–nd), из которой следует, что S = P (1–nd).
Приравняем множители наращения, подставив n=t/K (t – срок наращения процентов в днях, K – временная база):
(1+(t/365)i)=1/(1–(t/360)d),
откуда получаем формулу эквивалентного перехода
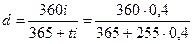 =0,30835, т.е. 30,835%
=0,30835, т.е. 30,835%
Пример 26. Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%?
Решение. Из равенства еd = (1+j/m)m следует d = m ln (1+j/m)= 4·ln (1+0,2/4)=0,19516, т.е. 19,516%.
Формулы эквивалентности дискретных и непрерывных ставок позволяют расширить применение непрерывных процентов. Непрерывные проценты во многих сложных расчетах позволяют существенно упростить выкладки. Вместе с тем такие ставки непривычны для практика, поэтому, используя формулы эквивалентности, нетрудно представить полученные результаты в виде общепринятых характеристик.
Дата добавления: 2021-02-19; просмотров: 521;











