Начисление сложных годовых процентов
В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления, а присоединяются к сумме долга, применяют сложные проценты. База для начисления сложных процентов, в отличие от простых, не остается неизменной – она увеличивается с каждым шагом во времени. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая служила базой для их начисления, часто называют капитализацией процентов, а способ вычисления процентных платежей по сложным процентам – вычислением "процента на процент".
Найдем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в году. Пусть первоначальная сумма долга равна P, в конце первого года сумма долга с присоединенными процентами составит P+Pi=P(1+i), к концу второго года – P(1+i)(1+i)=P(1+i)2 и т.д. К концу n-го года первоначальная сумма достигнет величины
S=P(1+i)n, (2.1)
где S – наращенная сумма, i – годовая ставка сложных процентов, n – срок ссуды. Величину (1+i)n называют множителем наращения по сложным процентам.
Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен Р, а знаменатель – (1+i).
Пример 10. Ссуда величиной 10000 рублей выдана на 2 года при ставке сложных процентов, равной 14% годовых. Определить величину процентного платежа и сумму накопленного долга.
Решение. По формуле (2.1) находим:
S=P(1+i)n=10000·(1+0,14)2=10000·1,2996=12996 руб. – наращенная сумма.
Проценты за 2 года: I=S-P=12996-10000=2996 руб.
Отметим, что при сроке n>1 наращение по сложным процентам дает больший результат, чем по простым, а при n<1 – наоборот. В этом нетрудно убедиться на конкретных числовых примерах (см. таб. 3). Наибольшее превышение суммы, наращенной по простым процентам, над суммой, наращенной по сложным процентам, (при одинаковых процентных ставках) достигается при n=1/2.
Таблица 3
Сравнение множителей наращения, iпр=iсл=12%
| Множители наращения | Срок ссуды | ||||||
| 30 дн. | 120 дн. | 180 дн. | 1 год | 2 года | 5 лет | 10 лет | |
| 1+niпр | 1,010000 | 1,040000 | 1,060000 | 1,120000 | 1,240000 | 1,600000 | 2,200000 |
| (1+iсл)n | 1,009489 | 1,038499 | 1,058301 | 1,120000 | 1,254400 | 1,762342 | 3,105848 |
Переменные ставки. Формула (2.1) предполагает постоянную ставку на протяжении всего срока начисления процентов. В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид
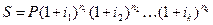 ,
,
где i1, i2, …, ik – последовательные значения ставок процентов, действующих в периоды nl, n2, …, nk соответственно.
Пример 11. Ссуда величиной 15000ден. ед. выдана на 4 года. В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года и наращенную сумму к концу срока ссуды.
Решение. Множитель наращения составит (1+0,3)2·(1+0,28)·(1+0,25)=2,704
Наращенная сумма S=15000·2,704=40560 ден. ед.
2.2. Наращение процентов m раз в году. Номинальная и эффективная ставки процентов.
Номинальная ставка. Проценты, как правило, капитализируются не один, а несколько раз в году – по полугодиям, кварталам и т.д. При начислении процентов несколько раз в году можно воспользоваться формулой (2.1). Параметр n в этих условиях будет означать число периодов начисления, а под ставкой i следует понимать ставку за соответствующий период. На практике, как правило, в контрактах фиксируется не ставка за период начисления, а годовая ставка, одновременно указывается период начисления процентов. Например, "18% годовых с ежемесячным начислением процентов".
Пусть годовая ставка сложных процентов равна j, число периодов начисления в году – m. Тогда каждый раз проценты начисляются по ставке j/m. Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по формуле
S=P(1+ j/m)N, (2.2)
где N – число периодов начисления (N=nm).
Пример 12. Ссуда величиной 10000 рублей выдана на 2 года. Номинальная ставка сложных процентов – 14% годовых. Определить сумму накопленного долга, если начисление процентов производится: (1) раз в году; (2) раз в полугодие; (3) раз в квартал.
Решение. (1) m=1, j/m=0,14, N=2. S=P(1+ j/m)N=10000·(1+0,14)2=10000·1,2996= =12996 руб. – наращенная сумма.
(2) m=2, j/m=0,14/2=0,07, N=2·2=4. S=10000·(1+0,07)4=10000·1,3108=13108 руб.
(3) m=4, j/m=0,14/4=0,035, N=2·4=8. S=10000·(1+0,035)8=10000·1,3168=13168 руб.
Как видно из приведенного выше примера, при одной и той же номинальной процентной ставке, но разной частоте начисления процентов результаты отличаются: чем чаще начисляются проценты, тем быстрее идет процесс наращения. По этой причине номинальная процентная ставка не может служить универсальным измерителем эффективности финансовых операций.
Эффективная ставка. Эта ставка измеряет тот реальный относительный доход, который получают в целом за год. Т.е. эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m.
Обозначим эффективную ставку через iэ. Если проценты капитализируются m раз в год, каждый раз со ставкой j/m, то, по определению, можно записать равенство для соответствующих множителей наращения:
(1+iэ)n=(1+ j/m)nm,
где iэ – эффективная ставка, а j – номинальная. Отсюда получаем, что связь между эффективной и номинальной ставками выражается соотношением
iэ=(1+ j/m)m-1.
Обратная зависимость имеет вид
j=m((1+iэ)1/m-1)= 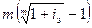 .
.
Надо заметить, что при m>1 эффективная ставка больше номинальной.
Замена в договоре номинальной ставки j при m-разовом начислении процентов на эффективную ставку iэ не изменяет финансовых обязательств участвующих сторон. Обе ставки эквивалентны в финансовом отношении.
Пример 13. Рассчитать эффективные процентные ставки для примера 12 и найти накопленную сумму долга.
Решение. (1) m=1, iэ=0,14. S=P(1+iэ)2=10000·1,142=12996 руб.
(2) m=2, iэ=(1+ j/m)m-1=(1+0,14/2)2-1=0,1449 или 14,49%. S=10000·1,14492= =13108 руб.
(3) m=4, iэ=(1+0,14/4)4-1=0,1475 или 14,75%. S=10000·1,14752=13168 руб.
Пример 14. Определить, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 12% годовых.
Решение. m=4, iэ=0,12. Тогда j=m((1+iэ)1/m-1)=4·((1+0,12)1/4-1)=4·(1,02874-1)= =0,11495, т.е. 11,495%.
Начисление процентов при дробном числе лет. Часто срок ссуды измеряется дробным числом периодов начисления. В этом случае при m-разовом начислении процентов в году наращенную сумму можно рассчитывать несколькими способами, приводящими к различным результатам:
1) По формуле (2.2) сложных процентов (общий метод)
S=P(1+j/m)N,
где N – число (возможно дробное) периодов начисления;
2) На основе смешанного метода, который предполагает начисление процентов за целое число лет по формуле сложных процентов, за дробную часть срока – по формуле простых процентов:
S=P(1+j/m)а(1+bj/m),
где a – целое число периодов начисления (a=[N] – целая часть числа N), b – оставшаяся дробная часть (b=N-a);
3) В правилах ряда коммерческих банков для некоторых операций проценты начисляются только за целое число лет или других периодов начисления. Дробная часть периода отбрасывается.
Пример 15. Размер ссуды 20 тыс. ден. ед., которая предоставлена на 28 месяцев. Номинальная ставка равна 60% годовых. Начисление процентов ежеквартальное. Вычислить наращенную сумму в трех ситуациях: 1) дробная часть игнорируется; 2) на дробную часть начисляются сложные проценты, 3) на дробную часть начисляются простые проценты.
Решение. Начисление процентов ежеквартальное. Всего имеется 28/3= 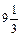 кварталов.
кварталов.
1) S=20·(1+0,6/4)9=20·1,159=20·3,5179=70,358 тыс. ден. ед.;
2) 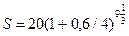 =20·3,6856=73,713 тыс. ден. ед.;
=20·3,6856=73,713 тыс. ден. ед.;
3) S=20·(1+0,60/4)9·(1+(1/3)·(0,6/4))= 20·3,5179·1,05=73,876 тыс. ден. ед.
Из сопоставления наращенных сумм видим, что наибольшего значения она достигает в третьем случае, т.е. при применении смешанного метода.
Дата добавления: 2021-02-19; просмотров: 563;











