Расчет срока ссуды и размера процентных ставок

В ряде практических задач начальная (P) и конечная (S) суммы заданы контрактом, и требуется определить либо срок платежа, либо процентную ставку, которая в данном случае может служить мерой сравнения с рыночными показателями и характеристикой доходности операции для кредитора. Указанные величины нетрудно найти из исходных формул наращения и дисконтирования (для простых процентов эти задачи рассмотрены в п. 1.8.).

Срок ссуды.Рассмотрим задачу расчета n для различных условий наращения процентов и дисконтирования.

При наращении по сложной годовой ставке i из исходной формулы наращения (2.1) следует, что

,

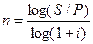где логарифм можно взять по любому основанию, поскольку он имеется и в числителе, и в знаменателе.

При наращении по номинальной ставке процентов j m раз в году из формулы (2.2) получаем:

.

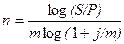При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке f m раз в году из формул (2.3) и (2.4) соответственно получаем:

;

.

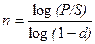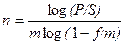При наращении по постоянной силе роста, исходя из формулы (2.6) получаем:

.

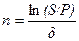Пример 22. За какой срок в годах сумма, равная 75 тыс. ден. ед., достигнет 200 тыс. ден. ед. при начислении процентов по сложной ставке 12% раз в году и поквартально?

Решение. По формулам для вычисления срока при наращении по сложным ставкам наращения получим:

n=(log(200/75)/log(1+0,12))=3,578 года;

n=(log(200/75)/(4·log(1+0,12/4))=3,429 года;

Расчет процентных ставок. Из тех же исходных формул, что и выше, получим формулы для расчета ставок при различных условиях наращения процентов и дисконтирования.

При наращении по сложной годовой ставке i из исходной формулы наращения (2.1) следует, что

i=(S/P)^1/n –1= .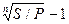

При наращении по номинальной ставке процентов m раз в году из формулы (2.2) получаем:

j=m((S/P)^1/mn –1)= .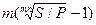

При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке f m раз в году из формул (2.3) и (2.4) соответственно получаем:

d =1– (P/S)^1/n = ;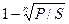

f = m(1– (P/S)^1/mn = .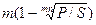

При наращении по постоянной силе роста, исходя из формулы (2.6), получаем:

.

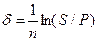Пример 23. Сберегательный сертификат куплен за 100 тыс. ден. ед., его выкупная сумма – 160 тыс. ден. ед., срок 2,5 года. Каков уровень доходности инвестиции в виде годовой ставки сложных процентов?

Решение. Воспользовавшись полученной формулой для годовой ставки i, получим: i=(160/100)^1/2,5–1=1,2068–1=0,20684, т.е. 20,684%.

Пример 24. Срок до погашения векселя равен 2 годам. Дисконт при его учете составил 30%. Какой сложной годовой учетной ставке соответствует этот дисконт?

Решение. По данным задачи P/S=0,7. Тогда d=1– 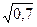=0,16334, т.е. 16,334%.