Непрерывные марковские цепи

На практике часто встречаются ситуации, когда система имеет конечное число дискретных состояний, а переходы между состояниями происходят в произвольные моменты времени. Например, отказы аппаратуры могут произойти в любой случайный момент времени.

Случайный процесс с непрерывным временем называется непрерывной марковской цепью, если поведение системы после произвольного момента времени t зависит только от состояния в этот момент времени и не зависит от истории процесса, предшествующей моменту t (соблюдается принцип отсутствия последействия).

Очень часто на практике интервалы времени между двумя переходами между состояниями системы подчинены показательному закону распределения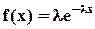

Для непрерывной марковской цепи определим вероятности всех состояний системы для любого момента времени p_i(t), i=1, 2,…, N. Так как для любого момента t все состояния образуют полную группу событий, то

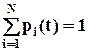
Пусть система в момент времени t находится в состоянии S_i. Рассмотрим элементарный промежуток времени Dt, примыкающий к моменту времени t. Вероятность перехода из состояния S_i в S_j за промежуток Dt обозначим p_ij(Dt). Назовем плотностью вероятности перехода величину l_ij,определяемую так:

,

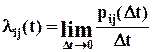то есть, при малых Dtвероятность перехода p_ij(Dt) » l_ij(t) Dt.

Если все плотности вероятностей перехода не зависят от t, то такой марковский процесс называется однородным: l_ij(t) = l_ij = const (и неоднородным – в противном случае). При этом для случая, когда интервал времени между переходами системы распределен по показательному закону, плотность вероятности перехода равна параметру lпоказательного закона.

Пусть известны плотности вероятностей переходов l_ij для всех пар состояний S_i и S_j. Определим вероятности состояний системы p_i(t). Для момента времени t+Dt справедливо соотношение:

.

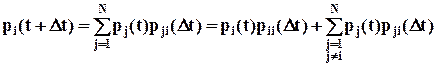Из свойства матрицы переходных вероятностей (сумма вероятностей по строке равна 1) следует:

.

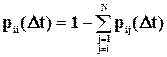Подставив это в предыдущее выражение, получим:

,

.

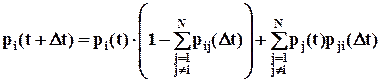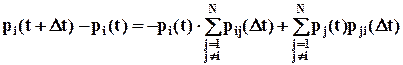Разделим обе части равенства на Dt и устремим его к нулю, получаем:

.

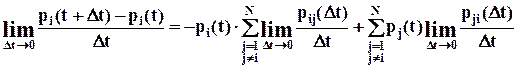Получили систему дифференциальных уравнений А.Н.Колмогорова:

, .

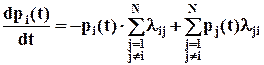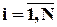Интегрирование этой системы по времени позволит вычислить функции p_i(t). При этом должно соблюдаться условие нормировки.

Колмогоров Андрей Николаевич (1903 - 1987). Великий русский ученый, один из крупнейших математиков XX столетия, член Национальной Академии наук США и американской Академии искусств и наук, член Нидерландской Королевской академии наук, Академии наук Финляндии, Академии наук Франции, Германской академии естествоиспытателей "Леопольдина", Международной академии истории наук и национальных академий Румынии, Венгрии и Польши, почетный член Королевского статистического общества Великобритании, Лондонского математи­ческого общества, Международного статистического института и Математического общества Индии, иностранный член Американского философского общества, Американского метеорологического общества, лауреат самых почетных научных премий: премии П.Л.Чебышева и Н.И.Лобачевского АН СССР, Международной премии фонда Больцано и Международной премии фонда Вольфа, а также государственной и Ленинской премии, награжденный 7-ю орденами Ленина, медалью "Золотая Звезда" Герой Социалистического труда академик Андрей Николаевич Колмогоров сам себя всегда называл "просто профессор Московского университета". На протяжении почти полувека А.Н.Колмогоров был общепризнанным лидером в теории вероятностей. Вместе с А.Я. Хинчиным и многими своими учениками он внес значительный вклад в развитие теории информации. К середине 50-х гг. именно А.Н.Колмогоров предложил наиболее общее определение количества информации в вероятностном смысле, а в дальнейшем развил и другой подход, так называемую алгоритмическую теорию информации, в котором под энтропией понималась сложность объекта, равная сложности алгоритма, описывающего объект.

В эргодических марковских цепях существует установившийся режим, при котором вероятности не меняются с течением времени. Следовательно, p_i(t)=p_i. Производные в системе дифференциальных уравнений Колмогорова при этом равны 0 и система Колмогорова становится сходной с системой для нахождения стационарных вероятностей для дискретных систем.

Вопросы и задачи к главе 2

1. На телеграфе установлен автоматизированный пункт передачи сооб­щений[2], работающий в режиме самообслуживания. Отправителю предоставляется рабочее место с микроЭВМ, позволяющей набрать нужный текст, отобразить его на экране и отредактировать. Набор текста начинается с клавиши «Ввод». Если операции ввода и редактирования отправителем выполнены, то по нажатию специальной клавиши «Завершение» текст запоминается и начинает обрабатываться машиной (распознается адрес, подсчитывается количество символов, определяется наличие признаков срочности телеграммы и т.п.). После завершения обработки на экране появляется символ готовности к передаче. Пользователь может нажать клавишу «Передача» или клавишу «Сброс». В первом случае состоится передача текста, во втором – текст будет удален из памяти ЭВМ и система придет в исходное состояние.

Дать теоретико-множественное описание системы.

Решение.Определим входы, выходы, состояния системы и связи между этими множествами. В качестве входов можно определить вектор из четырех булевских переменных: U = {u₁, u₂, u₃, u₄}, принимающих значение Истина, если нажаты клавиши «Ввод», «Завершение», «Передача» и «Сброс» соответственно. Состояниями в этом случае будут две булевских величины X = {х₁, х₂}. Первая принимает значение Истина, если аппарат находится в режиме редактирования текста, и Ложь, если аппарат находится в режиме простоя. Вторая принимает истинное значение, если аппарат занят, и ложное – в случае простоя аппарата. Выходом системы будет логическая величина у: происходит (Истина) или не происходит (Ложь) передача телеграммы. Функционирование такой системы можно описать таблицей истинности.

Эту же систему можно описать, используя функции алгебры логики: х₁ = u₁; х₂ = u₁Úu₂Úu₃; у = х₂Ùu₃.

2. «Министерский» телефонный аппарат имеет телефонную трубку, N кнопок для вызова абонентов, память на один телефонный номер, кнопку повторного вызова последнего набранного абонента и кнопку стирания номера абонента из памяти. Вызов абонента осуществляется при поднятой телефонной трубке нажатием одной из N клавиш, соответствующей требуемому абоненту. При соединении с абонентом его номер автоматически заносится в память аппарата.

Дать теоретико-множественное описание системы.

3. Игра в большой теннис. Вероятность выигрыша подачи игроком А – 0.6, вероятность выигрыша подачи игроком В – 0.4.

Описать один гейм матча в виде марковской цепи.

4. Укажите положительные и отрицательные стороны применения качественных и количественных методов описания систем.

5. Какие из подходов к описанию систем применены, по-вашему, в следующих случаях: принципиальная электрическая схема прибора; рецепт приготовления борща; уравнения, описывающие движение планет Солнечной системы; запись логической функции; схема плана боевой операции; нотация шахматной партии; нотная запись мелодии; организационная схема управления предприятием; медицинская карта - история болезни человека; конституция государства; блок-схема алгоритма.

6. Чем непрерывная марковская цепь отличается от дискретной?

7. Что значит «описать систему в виде цепи Маркова»?

8. Какую роль играют обратные связи в управлении системами?

9. Чем оптимальное управление отличается от программного управления?

10. Какие допущения вносятся при описании системы в виде кусочно-линейного агрегата?

[1] Пример взят из кн. Вероятностные методы в вычислительной технике/ А.В.Крайников, Б.А.Курдиков, А.Н.Лебедев и др. – М.: Высш. шк., 1986.

[2] Сюжет примера взят из кн.: Дегтярев Ю.И. Системный анализ и исследование операций. – М.: Высш. шк., 1996.