Фазовый синхронизм в одноосных кристаллах

Итак, согласно предыдущему параграфу, используя нелинейные среды в принципе можно преобразовать частоту исходной световой волны.

Известно, что в среде с дисперсией показателя преломления световые волны различной частоты имеют различные скорости распространения.

Если в кристалле распространяется плоская волна с частотой ω

E₁ = E₁₀cos(ωt –k₁z), (7.12)

и ее вторая гармоника с частотой 2ω: E₂ = E₂₀cos(2ωt –k₂z), (7.13)

то соответствующие этим волнам фазовые скорости равны:

u₁=с/n_w=w /k₁ и u₂=с/n_2w=2w /k₂. (7.14)

Вследствие дисперсии показателя преломления в среде n_w≠n_2w, и, следовательно, u₁ ≠u₂.

Из неравенства фазовых скоростей с учетом (7.15) получаем k₁≠k₂, или,

2 k₁-k₂=Δk (7.15)

Эта разность волновых чисел Δk носит название волновой расстройки.

Амплитуда волны второй гармоники в точке z, генерируемой в среде с дисперсией, дается выражением: A_2w(z)=(2A/Δk)sin(Δkz/2), (7.16)

и она достигает своего первого максимума на расстоянии, называемой длиной когерентности: l_ког=p/Δk=l/4(n_w -n_2w), (7.17)

где l=(2pс/w) -длина волны основной волны в вакууме. Выбрав, например, l»1мкм и Dn»10^-2, получим l_ког»25мкм.

Экспериментальная зависимость интенсивности второй гармоники в кристалле кварца от угла поворота пластинки показана на рис.7.3.

Рис.7.3. Зависимость интенсивности второй гармоники в кристалле кварца от угла поворота пластинки.

Как видим из этого рисунка, после достижения максимального значения интенсивность второй гармоники начинает уменьшаться.

Если z>>l_ког, то амплитуда волны второй гармоники имеет характер биений согласно выражению (7.16). Однако повышение эффективности преобразования во второй гармонике возможно при выполнении так называемого условия фазового синхронизма, если выполняется условие: Δk=0, или k₂=2k₁. (7.18)

Условие (7.18) называется условием волновогоилифазового синхронизма, и оно эквивалентно условию равенства фазовых скоростей волны второй гармоники и исходной волны.

Выполнить условие равенства фазовых скоростей для взаимодействующих волн удается в оптически анизотропных кристаллах с двулучепреломлением. Известно, что в одноосном кристалле могут распространяться две монохроматические волны ортогональных поляризаций (обыкновенная и необыкновенная) с одинаковыми частотами, но с разными фазовыми скоростями, т.е. с разными показателями преломления. Рассмотрим сечение индикатрисы показателя преломления отрицательного одноосного кристалла (n_o>n_e) для волны основной частоты w и ее второй гармоники частоты 2w.

Как видно из рисунка 7.4., в направлениях ОА, образующих угол q_c с оптической осью Z, выполняется равенство показателей преломления обыкновенной волны на частоте w и необыкновенной волны на частоте 2w

т.е.: n_w^о=n_2w^e . (7.19)

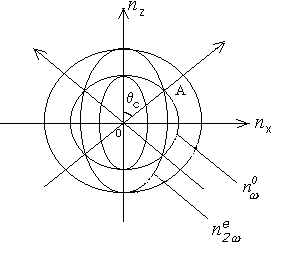
Рис.7.4. Сечение оптической индикатрисы отрицательного одноосного кристалла для обыкновенной волны частоты w и необыкновенной волны частоты 2ω.

Равенство (7.19) является условием фазового синхронизма для генерации второй гармоники. Для выполнения синхронизма волновые векторы должны быть ориентированы по направлению ОА. Эти направления называются направлениями синхронизма, а угол q_с - углом синхронизма. Показатель преломления для необыкновенной волны можно изменять, меняя угол между волновой нормалью и оптической осью и вычислить из выражения n^e(q)=n_en_о/[n_о²-(n_о²-n_e²)cos²q]^1/2 , (7.20)

где n₀ и n_e- главные значения показателя преломления на частоте w.

Используя выражение (7.20) можно легко вычислить угол синхронного взаимодействия волн в нелинейном кристалле.