Лекция 8. Электроны в кристаллах

Квантовая теория электропроводности металлов. Уровень Ферми. Элементы зонной теории кристаллов. Явление сверхпроводимости с точки зрения теории Ферми-Дирака. Электропроводность полупроводников. Понятие о дырочной проводимости. Собственные и примесные полупроводники. Понятие о p-n- переходе. Собственная проводимость полупроводников. Примесные полупроводники. Электромагнитные явления на границе раздела сред. p-n- переход. Фотопроводимость полупроводников. Люминесценция вещества. Термоэлектрические явления. Явление Зеебека. Эффект Пельтье. Явление Томсона.

8.1. Квантовая теория электропроводности металлов.
Уровень Ферми. Элементы зонной теории кристаллов

Классическая электронная теория проводимости металлов даёт удовлетворительное качественное согласие с экспериментом. Однако она приводит к значительному расхождению с опытом при объяснении ряда важнейших законов и явлений, таких, как:

а) закон зависимости удельного электрического сопротивления от температуры;

б) закон Дюлонга и Пти;

в) закон зависимости теплоемкости металлов и сплавов от температуры;

г) явления сверхпроводимости.

Так, например, согласно классической электронной теории проводимости металлов свободные электроны проводимости обмениваются энергией с кристаллической решеткой только при соударениях, поэтому атомная теплоемкость металла C_m должна складываться из теплоемкостей кристаллической решетки C_mк и теплоемкости электронного газа C_mэ, т.е.

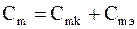. (8.1)

Теплоемкость кристаллической решетки

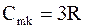. (8.2)

Для теплоемкости электронного газа имеем

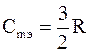. (8.3)

Таким образом, согласно классической электронной теории проводимости металлов для атомной теплоемкости металлов и сплавов имеем

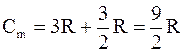. (8.4)

Согласно же закону Дюлонга и Пти атомная теплоемкость металлов и диэлектриков, у которых нет свободных электронов проводимости, существенно не отличается и равна

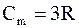. (8.5)

Закон Дюлонга и Пти подтверждается экспериментально.

Ограниченность классической теории проводимости металлов является следствием того, что она рассматривает совокупность свободных электронов как идеальный классический электронный газ, подчиняющейся некоторой функции (распределению Больцмана), характеризующей вероятность их нахождения в единице объема с определенной энергией и при данной температуре:

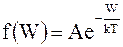, (8.6)

где W – энергия электрона;

T – абсолютная температура;

k – постоянная Больцмана;

A – коэффициент, характеризующий состояние электронов в целом.

Из формулы (8.6) видно, что при T®0 и W¹0 функция 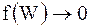. Это означает, что полная энергия электронов проводимости может принимать любые значения. Каждый электрон отличается от других. Он индивидуален. При этом все электроны должны находится на нулевом уровне, и в каждом состоянии с данной энергией может находиться их неограниченное количество. Это противоречит экспериментальным данным. Следовательно, функция распределения (8.6) не пригодна для описания состояния электронов в твердых телах.

Для устранения противоречий немецкий физик Зоммерфельд и советский физик-теоретик Я. И. Френкель для описания состояния электронов в металлах предложили применять принцип Паули, сформулированный ранее для электронов в атомах. В металле, как и в любой квантовой системе, на каждом энергетическом уровне могут находиться не более двух электронов, имеющих противоположные спины – механические и магнитные моменты.

Описание движения свободных электронов проводимости в квантовой теории осуществляется статистикой Ферми-Дирака, которая учитывает их квантовые свойства и корпускулярно - волновые свойства.

Согласно этой теории импульс (количество движения) и энергия электронов проводимости в металлах могут принимать только дискретный ряд значений. Иначе говоря, существуют определенные дискретные значения скорости электронов и энергетические уровни.

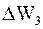Эти дискретные значения образуют так называемые разрешенные зоны, они разделены друг с другом запрещенными зонами (рис. 8.1). На рисунке прямые горизонтальные линии – энергетические уровни; – ширина запрещенной зоны; А, В, С – разрешенные зоны.

Принцип Паули в данном случае реализуется так: на каждом энергетическом уровне может быть не более 2-х электронов с противоположными спинами.

Заполнение энергетических уровней электронами носит не случайный характер, а подчиняется распределению Ферми-Дирака. Распределение определяется плотностью вероятности заселения уровней :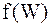

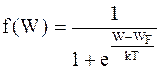(8.7),

где 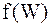– функция Ферми-Дирака;

W_F – уровень Ферми.

Уровень Ферми – это наиболее высокий заселенный уровень при Т=0.

Графически функцию Ферми-Дирака можно представить так, как показано на рис. 8.2.

Значение уровня Ферми зависит от типа кристаллической решетки и химического состава. Если 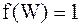, то уровни, соответствующие данной энергии, заселены. Если 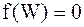, то уровни свободны. Если 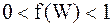, то такие уровни могут быть как свободными, так и заселенными.

При 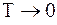функция Ферми-Дирака становится разрывной функцией, а кривая 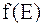– ступенькой. Чем больше 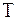, тем более пологий спад кривой 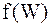. Однако при реальных температурах область размытости функции Ферми-Дирака составляет несколько kТ.

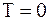При температуре , если 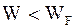, то 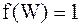, что означает - все уровни с такими энергиями заняты. Если 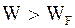, то 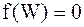, т.е. все более высокие уровни не заселены (рис.8.3).

Уровень Ферми значительно превосходит энергию теплового движения, т.е. W_F>>kT. Большое значение энергии электронного газа в металлах обусловлено принципом Паули, т.е. имеет нетепловое происхождение. Ее нельзя отнять за счет понижения температуры.

При 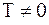функция Ферми-Дирака становится непрерывной. Если 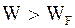на несколько kТ, единицей в знаменателе можно пренебречь и тогда

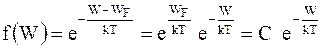. (8.8)

Таким образом, распределение Ферми-Дирака переходит в распределение Больцмана.

В металлах при T¹0 K функция f(W) в первом приближении практически не изменяет своего значения.

Степень заполнения электронами энергетических уровней в зоне определяется заполнением соответствующего атомного уровня. Например, если какой-то уровень атома полностью заполнен электронами в соответствии с принципом Паули, то образующаяся из него зона также полностью заполнена. В этом случае можно говорить о валентной зоне, которая полностью заполнена электронами и образована из энергетических уровней внутренних электронов свободных атомов, и о зоне проводимости (свободной зоне), которая либо частично заполнена электронами, либо свободна и образована из энергетических уровней внешних ²коллективизированных² электронов изолированных атомов (рис. 8.4).

В зависимости от степени заполнения зон электронами и ширины запрещенной зоны возможны следующие случаи. На рис. 8.5 самая верхняя зона, содержащая электроны, заполнена лишь частично, т.е. в ней имеются вакантные уровни. В данном случае электрон, получив сколь угодно малую энергию (например, за счет теплового воздействия или воздействия электрического поля), сможет перейти на более высокий энергетический уровень той же зоны, т.е. стать свободным и участвовать в проводимости. Внутризонный переход вполне возможен в том случае, когда энергия теплового движения гораздо больше разности энергий между соседними уровнями зоны. Таким образом, если в твердом теле имеется частично заполненная электронами зона, то это тело всегда будет проводником электрического тока. Это характерно для металлов и их сплавов.

Проводником электрического тока твердое тело может быть и в том случае, когда валентная зона перекрывается свободной зоной. Появляется не полностью заполненная зона (рис. 8.6), которую иногда называют ²гибридной². ²Гибридная² зона заполняется валентными электронами лишь частично. Перекрытие зон наблюдается в щелочно-земельных элементах.

С точки зрения теории Ферми-Дирака, заполнение электронами зон происходит следующим образом. Если энергия электронов W>W_F, то тогда при T=0 функция распределения f(W)=0, а это означает, что электронов на уровнях, расположенных за уровнем Ферми, нет.

Если энергия электронов W<W_F, то при Т=0 функция распределения f(W)=1, а это достоверность, т.е. электроны обязательно находятся на уровнях перед уровнем Ферми, или уровни перед уровнем Ферми заполнены.

При T¹0 электронам передаётся тепловая энергия ~kT, а следовательно, электроны с низших уровней могут перейти на уровень выше уровня Ферми. Происходит тепловое возбуждение электронов проводимости.

Все уровни валентной зоны заполнены. Однако все электроны не способны получить дополнительную энергию для энергетического скачка. Только небольшая часть электронов, заселяющих область "размытости" функции Ферми-Дирака порядка нескольких kТ, может оставить свои уровни и перейти на более высокие (рис. 8.7). Следовательно, только небольшая часть свободных электронов, находящаяся в зоне проводимости, участвует в создании тока и может вносить вклад в теплоемкость металла. Вклад электронного газа в теплоемкость незначителен, что согласуется с законом Дюлонга и Пти.

Повышение энергии электронов проводимости может произойти не только за счет ²теплового² воздействия, но и за счет действия электрического поля (разности потенциалов), в результате чего они приобретут упорядоченное движение.

Если ширина запрещенной зоны кристалла порядка нескольких электрон-вольт, то тепловое движение не может перевести электроны из валентной зоны в зону проводимости и кристалл является диэлектриком, оставаясь им при всех реальных температурах.

Если ширина запрещенной зоны кристалла порядка 1 эВ, т.е. достаточно узкая, то переход электронов из валентной зоны в зону проводимости возможен. Он может быть осуществлен либо за счет теплового возбуждения, либо за счет возникновения электрического поля. В этом случае твердое тело является полупроводником.

Различие между металлами и диэлектриками, с точки зрения зонной теории, состоит в том, что при 0 К в зоне проводимости металлов имеются электроны, а в зоне проводимости диэлектриков их нет. Различие между диэлектриками и полупроводниками определяется шириной запрещенных зон: для диэлектриков она довольно широкая (для NaCl, например, DW = 6 эВ), для полупроводников - достаточно узкая (для германия DW = 0,72 эВ). При температурах, близких к 0 К, полупроводники ведут себя как диэлектрики, так как перехода электронов в зону проводимости не происходит. С повышением температуры у полупроводников растет число электронов, которые за счет теплового возбуждения переходят в зону проводимости, т.е. электрическая проводимость полупроводников в этом случае увеличивается.

В квантовой теории электроны проводимости рассматриваются как частицы, обладающие волновыми свойствами, а их движение в металлах – как процесс распространения электронных волн, длина которых определяется соотношением де Бройля:

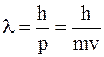, (8.9)

где h – постоянная Планка;

p – импульс электрона.

В совершенном кристалле, в узлах кристаллической решетки которого находятся неподвижные частицы (ионы), электроны проводимости (электронные волны) не испытывают взаимодействий (рассеяния), и такой кристалл, а следовательно, и металл, не оказывает сопротивления прохождению электрического тока. Проводимость такого кристалла стремится к бесконечности, а электрическое сопротивление – к нулю.

В реальных кристаллах (металлах и сплавах) имеются различные центры рассеяния электронов неоднородности (искажения), по размеру превосходящие длину электронных волн. Такими центрами являются флуктуации плотности искажения решетки, возникающие вследствие теплового движения (теплового колебания) ее узлов; различные дефекты структуры, атомы внедрения и замещения, примесные атомы и другие.

При беспорядочном движении электронов, среди узлов кристаллической решетки, имеются такие, которые в данный момент движутся навстречу друг другу. Расстояние между ними в этот момент времени оказывается меньше их расстояния в неподвижной решетке. Это приводит к увеличению плотности вещества в микрообъеме, охватывающем эти атомы (выше средней плотности вещества). В соседних областях возникают микрообъемы, в которых плотность вещества меньше её среднего значения. Эти отступления плотности вещества от среднего значения и представляют флуктуации плотности. В результате, в любой момент времени, металл (твердое тело) является микроскопически неоднородным. Эта неоднородность тем значительнее, чем меньше микрообъёмы (чем меньше атомов узлов охватывают микрообъёмы).

Как правило, размер таких микрообъёмов больше длины электронных волн, вследствие чего они являются эффективными центрами рассеяния этих волн. Поток свободных электронов в металле испытывает на них такое же рассеяние, какое испытывают световые волны на взвешенных частицах мутной среды. Это и является причиной электрического сопротивления абсолютно чистых металлов.

Рассеивающая способность металлов, обусловленная флуктуациями плотности, характеризуется коэффициентом рассеяния h_T.

Для свободных электронов коэффициент рассеяния

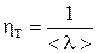, (8.10)

где <l> – средняя длина свободного пробега электрона.

Значение коэффициента рассеяния через характеристики теплового движения узлов кристаллической решетки и её упругие константы оказывается равным:

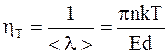, (8.11)

где n – число атомов (узлов) в единице объёма (в 1 м³);

E – модуль упругости;

d – параметр решетки;

T – абсолютная температура;

k – постоянная Больцмана.

Следовательно,

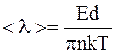. (8.12)

С учетом уравнения (8.12) удельная электропроводность металла

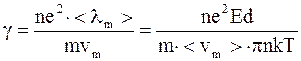. (8.13)

Из выражения (8.13) видно, что удельная электропроводность металлов обратно пропорциональна абсолютной температуре. Следовательно, удельное сопротивление металлов должно быть прямо пропорциональным абсолютной температуре, что хорошо согласуется с экспериментом. Выражение (8.17) было получено Зоммерфельдом на основании квантовой теории Ферми-Дирака.

Отличие выражения (8.13) от формулы 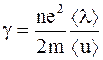состоит в том, что <l_m> в формуле Зоммерфельда – средняя длина свободного пробега электрона, обладающего энергией Ферми; <v_m> – скорость такого электрона. В формуле классической электронной проводимости металлов <l> – средняя длина свободного пробега, не зависящая от температуры, численно равная параметру решетки; <u> – средняя скорость теплового движения электрона проводимости. При этом <v_m> не зависит от температуры, а <u> – зависит.

Тепловые колебания узлов кристаллической решетки являются не единственными источниками искажения, приводящими к рассеянию электронных волн. Такими же источниками являются структурные всевозможные искажения (дефекты): примеси, деформация и т.д. Поэтому коэффициент рассеяния складывается из двух частей:

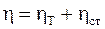, (8.14)

где h_T – тепловой коэффициент рассеяния;

h_ст = h_пр + h_д – коэффициент рассеяния за счет структурных искажений;

h_пр – коэффициент рассеяния за счет примесей;

h_д – коэффициент рассеяния за счет деформации.

Для слишком низких температур h_T ~ T (при низких температурах h_T ~ T⁵), в отсутствии деформации h_ст пропорционален концентрации примесей и не зависит от температуры, следовательно,

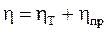. (8.15)

Тогда удельное электросопротивление можно определить так:

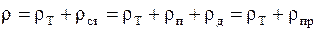. (8.16)

При T®0, r_T®0 и r®r_ст к так называемому остаточному сопротивлению, которое не исчезает при температуре, равной абсолютному нулю. Так как число электронов проводимости в металле не зависит от температуры, то вольтамперная характеристика металлического проводника имеет вид прямой линии.

8.2. Явление сверхпроводимости
с точки зрения теории Ферми-Дирака

Физическая сущность теории сверхпроводимости разработана Н.Н. Боголюбовым с сотрудниками и заключается в следующем.

Свободные электроны проводимости металлов образуют электронный газ, подчиняющийся статистике Ферми-Дирака. Между электронами действуют кулоновские силы отталкивания, которые в значительной степени ослаблены наличием поля положительных ионов узлов кристаллической решетки. Кроме того, они взаимодействуют с тепловыми колебаниями решетки, не прекращающимися даже при температуре 0 K. При таких взаимодействиях электроны, располагающиеся в узкой полосе, примыкающей к уровню Ферми, могут поглощать и излучать фононы (электронные волны). Происходит как бы обмен фононами, который приводит к возникновению сил притяжения между электронами проводимости. Если эти силы окажутся больше сил отталкивания, то под влиянием их электроны проводимости с противоположно направленными спинами связываются в пары с положительной энергией. Результирующий спин такой пары равен нулю. Энергия связи пары u_св зависит от направления спинов и максимальна для электронов, у которых собственные моменты количества движения (спины) антипараллельны.

При температуре 0 K электронные пары располагаются на основном энергетическом уровне, лежащем ниже уровня Ферми, который отделен от ближайшего уровня, отвечающего нормальному состоянию электронов в металле, энергетической щелью шириной u_с. По порядку величина энергии связи равна энергии теплового движения kT_к, соответствующей температуре перехода металла в сверхпроводящее состояние.

Минимальная энергия, которую может поглотить электрон, находящийся на основном уровне, равна u_с. При низкой температуре такую энергию от кристаллической решетки он получить не может. Поэтому электроны двигаются в этом случае без взаимодействия (торможения), не встречая сопротивления. Электрическое сопротивление в этом случае стремится к нулю.

Примеси, искажения кристаллической решетки, пластическая деформация металлов оказывают влияние лишь на резкость перехода вещества в сверхпроводящее состояние, но не уничтожают сам переход. Это говорит о том, что при переходе в сверхпроводящее состояние электроны проводимости (электронные волны) перестают взаимодействовать с узлами кристаллической решетки.

С повышением температуры ширина щели между энергетическими уровнями уменьшается, силы кулоновского отталкивания между электронами увеличиваются, электронные пары разрушаются, и электроны переходят с основного энергетического уровня на возбужденные уровни.

При температуре, равной W_к, энергия связи становится равной нулю (u_с = 0) и сверхпроводящее состояние исчезает.

8.3. Электропроводность полупроводников.
Понятие о дырочной проводимости.
Собственные и примесные полупроводники.
Понятие о p-n – переходе