Двухфотонное поглощение

Одним из фундаментальных нелинейных эффектов, который имеет разнообразное практическое значение, является многофотонное поглощение, в частности двухфотонное поглощение, при котором одновременно поглощаются два фотона, вследствие чего электрон (в атоме, молекуле) переходит с основного уровня E₁ на возбужденный уровень E₂ (рис.7.7.б, в). При этом предполагается, что между начальным и конечным состояниями другие связанные электронные состояния отсутствуют.

Рис.7.7. Процессы поглощения фотона в веществе: а) однофотонное поглощение фотона с энергией ђω₀; б) двухфотонное поглощение фотонов с энергией ђω₁; в) двухфотонное поглощение фотонов с энергиями ђω₂ и ђω₃..

Поскольку двухфотонное поглощение является нелинейным процессом, сечение поглощения для него намного порядков меньше сечения однофотонного поглощения. Тем не менее, двухфотонное поглощение легко наблюдается при использовании лазеров.

Процесс в средах можно рассмотреть феноменологически, описывая относительные изменение интенсивности I плоских волн при их прохождении через двухфотонно поглощающую среду. Пусть два пучка распространяются вдоль оси z среды и испытывают ослабление из-за двухфотонного поглощения, которое описывается уравнениями:

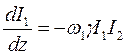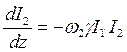, , (7.28)

где γ - коэффициент двухфотонного поглощения.

Связанные уравнения (7.28) можно решить аналитически, если учесть, что: .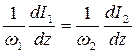

Это соотношение является следствием того, что в двухфотонном поглощении участвуют равные числа фотонов с частотами ω₁ и ω₂. Если I₁₀ и I₂₀ - интенсивности на входе в среду, то: (7.29)

Решение системы (7.28) можно получить, избавляясь от I₁ или I₂. Считая, что I₁₀ > I₂₀, находим: ,

, (7.30)

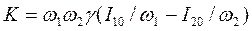
если I₁₀ >>I₂₀, то ослаблением волны I₁ можно пренебречь. В этом случае решение принимает вид: I₁≈I₁₀,, I₂=I₂₀exp(-Kz). (7.31)

Интерес представляет частный случай, когда ω₁=ω₂=ω. Тогда вместо (7.28) мы получим уравнение: 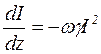, (7.32)

решение, которого имеет вид: 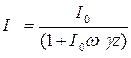. (7.33)

В случае слабого поглощения решение приводится к виду:

(7.34)

Из уравнения (7.34) экспериментально, по методу пропускания можно определить величину коэффициента двухфотонного поглощения γ для среды. Как видно выражение (7.34) не содержит микроскопических параметров среды, и поэтому невозможно в рамках данного метода предсказывать значение коэффициента двухфотонного поглощения γ для интересующих нас сред, что является основным недостатком.

Тем не менее, при рассмотрении многофотонных процессов методом теории возмущений, можно получить выражение для коэффициента двухфотонного поглощения в виде: 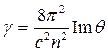, (7.35)

где n²=ε₁^1/2·ε₂^1/2 , - мнимая часть кубической нелинейной восприимчивости q, N –плотность молекул или элементарные ячейки в среде, M_fi –матричные элементы двухфотонных переходов под действием световых волн с частотами w₁ и w₂ (рис.7.7), r_i и r_f - населенности состояний i и f.

Рис. 7.8. Двухфотонное возбуждение системы из состояния |i> в состояние |f > через виртуальное промежуточное состояние |s>.

Как и ранее было отмечено, коэффициент двухфотонного поглощения γ прямо пропорционален мнимой части кубической нелинейной восприимчивости q, описывающей процесс двухфотонного поглощения.