Самофокусировка света

Физические причины этого нелинейного эффекта заключаются в изменении показателя преломления среды в сильном световом поле. Первый член в формуле (7.11) обладает периодичностью во времени такой же, как и у первичной волны. Однако это – нелинейный член, так как в качестве коэффициента при cos(wt-kх) стоит qE₀³. Таким образом, с кубичным по полю членом в нелинейной поляризации связано переизлучение на частоте падающей волны, но с амплитудой, пропорциональной коэффициенту q и кубу амплитуды падающей волны. Этот член обусловливает появление нелинейной поправки к показателю преломления среды. Электрическая индукция D на частоте w может быть представлена в виде:

D=e₀eE=e₀eЕ₀ cos(wt - kх)=[1+c+3/4qE₀²]e₀Е₀сos(wt-kх) (7.21)

и, следовательно, диэлектрическая проницаемость: e =n²=e_л + e₂Е₀² (7.22)

где e_л=1+c, а e₂=3/4q. Поскольку e₂Е₀²<<e_л, то (7.22) можно переписать в виде: n= n₀ +n₂E² (7.23)

где n₀=e_л^1/2. Таким образом, интенсивная световая волна изменяет показатель преломления среды. Добавочный член n₂E² тем больше, чем больше интенсивность падающей волны. Такие оптические эффекты принято называть самовоздействием световой волны. За счет появления нелинейных добавок к диэлектрической проницаемости e (или к показателю преломления n) световая волна изменяет собственную фазовую скорость , а также коэффициент поглощения в среде, причем эти изменения пропорциональны квадрату амплитуды волны Е₀². Это самовоздействие и приводит к эффекту самофокусировки света.

В поле ограниченного интенсивного светового пучка первоначально однородная среда в силу формулы (7.23) становится оптически неоднородной, следовательно, показатель преломления среды определяется теперь распределением интенсивности распространяющейся волны. Это приводит к явлению нелинейного преломлению света, характер которого определяется знаком нелинейной добавки n₂E². В среде с n₂>0 области максимальной интенсивности света являются одновременно и наиболее оптически плотными. В этом случае нелинейное преломление должно приводить к самофокусировке, так как периферийные лучи отклоняются в область, где поле максимально.

Чрезвычайно важным обстоятельством, выделяющим эффект самофокусировки среди других нелинейных оптических процессов, является его «лавинный» характер. Действительно, даже слабое увеличение интенсивности в некотором участке светового пучка в среде с n₂>0 приводит к концентрации лучей в этой области, следовательно, и к дополнительному возрастанию интенсивности, которое еще усиливает эффект нелинейного преломления и т.д. Однако пучок с конечным поперечным сечением должен одновременно дифрагировать. Если эффект самофокусировки окажется сильнее дифракции, только тогда пучок будет сфокусирован. Так как действие самофокусировки пропорционально n₂E², а действие дифракции обратно пропорционально квадрату радиуса пучка, следовательно, когда пучок сжимается из-за самофокусировки, одновременно усиливается действие и самофокусировки, и дифракции. Если последняя возрастает быстрее, то в некоторой точке дифракция берет верх над самофокусировкой и сфокусированный пучок, достигнув минимального сечения (фокальной точки) должен расходиться.

Условия самофокусировки. Пусть в нелинейной среде с n₂>0 распространяется цилиндрический пучок радиуса а (рис.7.5). Тогда вне пучка показатель преломления n₀=e_л^1/2 , а внутри пучка: n=n₀+n₂E². Лучи, падающие на границу пучка изнутри, совершают переход из среды оптически более плотной в среду оптически менее плотную; следовательно, при достаточно больших углах a для них возможен эффект полного внутреннего отражения. Критический угол соответствует лучу, угол наклона β₀ которого к оси пучка равен: β₀=arccos[n₀/(n₀+n₂E²)] (7.24)

Рис.7.5. Самоканализация интенсивного светового пучка в нелинейной среде.

Лучи с β>β₀ отклоняются от оси пучка, лучи с β<β₀ отклоняются к оси пучка. В пучке, фронт которого (поверхность равной фазы) на входе в нелинейную среду является плоским, угол β определяется дифракцией:

β_д=0,61λ₀/n₀2a (7.25)

Относительный вклад нелинейного преломления и дифракции в поведение такого пучка можно оценить, сравнивая углы β₀ и β_д. При β₀<β_д пучок расходится, однако темп дифракционной расходимости меньше, по сравнению с линейной средой. При β₀=β_д нелинейное преломление полностью компенсирует дифракционную расходимость луча; размеры и форма пучка остаются неизменными при распространении его в нелинейной среде. Пучок создаёт для себя своеобразный оптический волновод, по которому распространяется без расходимости. Этот режим называется режимом самоканализации волнового пучка. Пользуясь формулами (7.24) и (7.25), нетрудно убедиться, что условие (7.24) накладывает требование лишь на полную мощность пучка и величину нелинейности среды. Выражение для критической мощности самоканализирующегося пучка есть: β_д²/2=n₂E²_кр/n₀;

P_кр=λ²₀с(1,22)²/256n₂ . (7.26)

При β₀>β_д и, следовательно, при P>P_кр лучи отклоняются к оси пучка –происходит самофокусировка (рис.7.6.). В этом случае нелинейная среда действует как собирающая линза. Её фокусное расстояние можно оценить, пользуясь формулой (7.26). Вводя дифракционную длину R_д=ka²/2 ≈ a/β_д, получаем из (7.26), что условие β₀=β_д эквивалентно условию:

R_д=a/2 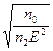≡R_нл. (7.27)

Величина R_нл, имеющая размерность длины, называется эффективной длиной самофокусировки.

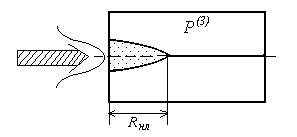
Рис.7.6. Самофокусировка интенсивного светового пучка
в нелинейной среде.

После самофокусировки луч превращается в тонкую нить на оси пучка. Для данной среды эта нить имеет постоянный диаметр в пределах ±20% и протяжённость равна нескольким сантиметрам. Диаметр нити равен диаметру фокального пятна, а интенсивность в нити – интенсивности в фокусе. Интенсивность света в такой нити может достигать десятков гигаватт на квадратный сантиметр.