Вывод расчетных формул для одноосных внутренних напряжений.

Разобьем сечение бруса на слои одинаковой толщины.

1. В пределах каждого слоя температура усредняется и равна Т_i

2. В пределах каждого слоя физико-механические характеристики постоянны и зависят от температуры слоя (a(Т_i), E(T_i), s_s(T_i))

В результате неравномерного нагрева каждый слой i удлинится на длину Dl_i. В соответствии с гипотезой плоского сечения, правый край повернется относительно левого на угол q.

Условие совместности деформации всех слоев бруса

Dl₁= Dl_i + (i-1)b; b пропорционально углу поворота q.

В любой полосе i абсолютное удлинение Dl_i складывается из свободного теплового удлинения a( Т_i )DT_i и деформации от внутренних напряжений e_i

Dl_i= aDT_i+e_i

Условие равновесия внутренних усилий

Ss_iF_i=0

Считая, что площадь всех слоев одинакова, получим

Ss_i=0 или Se_i E_i=0

Условие равновесия моментов от внутренних усилий

Ss_i F_i ^. i ^.d=0

Т.к. F и d постоянны, то получим

Ss_i ^. i =0 или Se_i E_i ^. i=0

Из условий совместности деформации получим

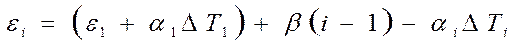
Подставим значение e_i в уравнения равновесия внутренних усилий

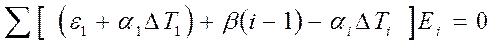
Находим значение величины e₁+ a₁DТ₁

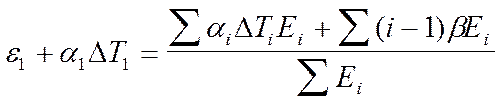
Отсюда найдем значение

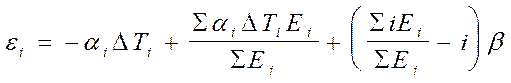
Подставим значение e_i в условие равновесия моментов и получим

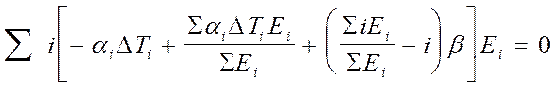
Введем для сокращения записи обозначения

Ro=SE_i ; R₁= SiE_i ; R₂=SE_i i² ; R_a = SE_i a_iDT_i ; R_a1 = Si×E_i a_iDT_i

.

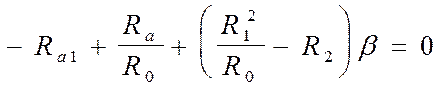Отсюда

.

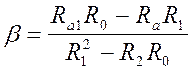Если b>0, то брус деформируется согласно схеме, если b< 0 – то в обратную сторону.

Напряжения в каждом слое вычисляются по формуле

s_i = e_i E_i .