Никакие два электрона в одном атоме не могут характеризоваться одинаковым набором всех четырех квантовых чисел n, l, m, s.

Внимательный читатель мог заметить, что на рисунке 2-16, показывающем электронные переходы в атоме лития, порядок заполнения уровней и подуровней вполне логичный: 1s, 2s, 2p, 3s, 3p, 3d, 4s … . Как показали спектры испускания, это характерно только для атомов c небольшим числом электронов. Впрочем, об этом редко вспоминают, потому что у самых легких элементов на 3-м и 4-м уровнях вообще нет электронов. С увеличением числа электронов в атоме подуровень 4s, как мы уже знаем, начинает заполняться раньше, чем 3d. А на более высоких уровнях такие "нарушения" становятся правилом. Можно воспользоваться уже освоенными нами квантовыми числами для того, чтобы уметь воспроизводить ряд заполнения электронами уровней и подуровней большинства атомов (1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d …) с помощью правила Клечковского:

Энергия уровней и подуровней возрастает в порядке увеличения суммы n + l, а при одном и том же значении этой суммы ниже располагаются уровни с меньшим n.

Но на практике гораздо легче не мучиться со сложением квантовых чисел, а использовать для реконструкции этого ряда схему длинной формы Периодической таблицы, с которой мы познакомимся в главе 4.

В модели Бора электрон рассматривался как частица. Его положение в пространстве, орбита и скорость описывались теми же методами, которые используются при вычислении траекторий планет. Но для космических тел не бывает "разрешенных" и "неразрешенных" орбит, а в атоме Бора могли быть только разрешенные (стационарные) орбиты. Находясь на этих орбитах, электрон почему-то не излучает энергию при движении вокруг заряженного ядра. Эта устойчивость электрона на стационарных орбитах так и оставалась необъяснимой.

В 20-х годах прошлого века французский физик Л. де Бройль выдвинул гипотезу о том, что электрон обладает свойствами не только частицы, но и волны. Впоследствии это удалось подтвердить экспериментально. Гипотеза де Бройля позволила изящно объяснить, почему электрон в атоме может существовать только на стационарных орбитах. Стационарными орбитами в атоме могут быть только такие орбиты, в которые укладывается целое число длин волн электрона. Такая волна называется "стоячей" (рис. 2-18).

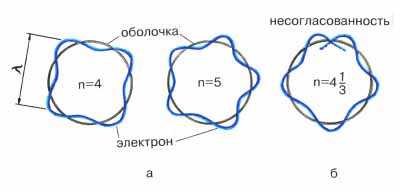
Рис. 2-18. Разрешенные (а) и неразрешенные (б) стоячие волны электрона на боровских орбитах. Стоячие волны на круговой орбите могут существовать только при условии, что длина орбиты равна целому числу длин волн. В случае (б) это условие не соблюдается и волна гасит сама себя. Такая модель наглядно показывает, что квантовое число n может быть только целым.

Появление гипотезы де Бройля открыло принципиальную возможность описывать электрон в атоме уже не как частицу, а как волну. Это в 1926 году сделал австрийский физик Э. Шредингер. Он применил к электрону в атоме математический аппарат, описывающий движение волны в трехмерном пространстве. Такое движение описывается математической функцией (её называют "пси"-функцией), в которую входят координаты трехмерного пространства x, y, z. Оказалось, что квадрат этой функции описывает уже не движение волны, а вероятностьобнаружить эту волну в точке пространства с координатами x, y, z. Так появилась возможность рассчитывать вероятность нахождения электрона-волны в разных точках пространства вокруг ядра.

Результаты решения уравнения Шредингера для атома водорода обычно приводятся в виде уже знакомых нам "электронных облаков": сферические s-облака (s-орбитали), гантелеобразные p-облака (p-орбитали) и т.д.

На рисунке мы видим изображения s- и p-орбиталей 2-го уровня, причем p-орбитали "пронизывают" s-орбиталь. Но разве могут области существования разных электронов пересекаться? Как может p-электрон существовать "внутри" s-электрона и может ли 1s-электрон находиться "внутри" 2s-электрона? Объяснение заключается в том, что до сих пор не удается решить уравнение Шредингера для атомов сдвумя и более электронами, поэтому мы вынуждены пользоваться результатами расчетов для одноэлектронных атомов - атома водорода, ионов He⁺, Li²⁺ и т.д. В этих системах электрон находится либо на s-орбитали, либо на p-орбиталях и никогда не встречается ситуация с одновременным нахождением нескольких электронов на разных орбиталях. Таким образом, для описания многоэлектронных атомов приходится применять одноэлектронное приближение волновой модели, не учитывающее взаимное влияние электронов. Это вынужденный и одновременно смелый шаг. Впрочем, он оказался оправданным - модель хорошо "работает" не только при описании свойств многоэлектронных атомов, но и в теории химической связи. Именно такое представление атомных орбиталей весьма пригодится вам при изучении органической химии - для описания электронного строения органических соединений и объяснения их химических свойств.

Но можно ли считать электрон исключительно волной? Разумеется, нет. Термин "корпускулярно-волновой дуализм" предполагает обязательное наличие у объекта (электрона) как свойств частицы, так и свойств волны. Интересно об этом рассуждали крупнейшие физики, стоявшие у истоков квантовой механики. Вот, например, выдержка из воспоминаний нобелевского лауреата В. Гейзенберга: «…Электрон всегда рисовался моему воображению в виде маленькой сферы. Я бывало говорил только одно: «Иногда, конечно, можно с пользой назвать его волной, но это не более чем способ разговора, а физическая реальность тут ни при чем». Характерно мнение другого замечательного физика - А. Зоммерфельда, высказанное в лекции «Современное состояние атомной физики» в Гамбургском университете в феврале 1927 года: «…В трехмерном пространстве электрон нельзя локализовать. Это подчеркивает Гейзенберг, а Шредингер иллюстрирует это, «размазывая» заряд электрона в сплошную пространственную массу. Лично я не верю в этот размазанный, растекающийся электрон уже потому, что вне атома электроны-корпускулы, обладающие большой скоростью, с несомненностью могут быть установлены экспериментом. С другой стороны, неоспоримый факт, что сплошные плотности Шредингера при расчете физических и химических действий атома оказывают неоценимую помощь и в этом смысле реальны в большей степени, нежели точечно локализованный электрон старой теории».

Нам необходимо понимать, что изображения орбиталей волновой модели - это не внешний вид электронов в атоме, а области вероятностинайти s-, p- или какой-либо другой электрон в пространстве вокруг ядра. Для того, чтобы такие области имели не слишком размытые границы, на рисунках показывают области с 95%-ной вероятностью обнаружить здесь электрон. Надо также помнить, что это области вероятности, рассчитанные в рамках данной модели атома. Поэтому, когда вы читаете в учебнике, что вспомогательное (оно же орбитальное, побочное, азимутальное) квантовое число l определяет форму электронного облака, то должны при этом понимать, что такое облако - не более чем абстрактное математическое построение в рамках волновой модели атома. Например, сейчас уже мало кто вспоминает, что в модели Бора-Зоммерфельда квантовое число l "заставляло" s-электроны двигаться по наиболее вытянутым, эллиптическим орбитам, в то время как орбиты p- и d-электронов оказывались близкими к круговым.

Модель Бора-Зоммерфельда очень красива и до сих пор используется художниками для создания символики, отражающей достижения современной физической науки. Ниже вы видите несколько таких примеров: герб города Дубна (здесь расположен один из крупнейших российских исследовательских центров), эмблема физического факультета Новосибирского университета, ледокол "Россия" с изображением электронной оболочки атома гелия в рамках "устаревшей" модели Бора-Зоммерфельда. Интересно, знал ли эту подробность художник, создававший эмблему? Для моряков встречных судов такой рисунок на борту ледокола означает лишь, что этот могучий корабль оснащен атомной силовой установкой.

Следует все же помнить, что термин "орбита" (из модели Бора) в волновой модели теперь полностью уступил место термину "орбиталь".Орбиталь имеет чисто вероятностный смысл и её просят не путать с орбитой, т.е. траекторией движения электрона.

В этом параграфе были упомянуты три важных составляющих современной электронной модели атома: принцип минимума энергии, правило Гунда, запрет Паули. Вместе с четырьмя квантовыми числами они позволят описывать электронную оболочку атома элемента, исходя лишь из порядкового номера этого элемента в таблице Менделеева.

Не следует относиться к построениям квантовой теории, как к окончательной, не подлежащей сомнению истине. Квантовая теория - это лишь модель такого сложного природного явления, каким является атом. Квантовая модель удобна тем, что позволяет предсказывать многие, даже еще не открытые свойства различных элементов. В этом ее преимущество перед многими предшествующими теориями строения материи.

В последующих главах мы будем пользоваться современной электронной моделью атома для объяснения таких сложных явлений, как возникновение химической связи, образование молекул, их пространственная форма, существование ионов и т.д. Мы также сможем предсказывать многие химические свойства элементов и их соединений. Наконец, мы объясним Периодический закон Д.И.Менделеева и увидим, насколько гармонично он сочетается с современной моделью атома, хотя был сформулирован в то время, когда Планк, Резерфорд и Бор еще не начинали свою работу.