ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ

Рассмотрим некоторые частные случаи пересечения поверхностей второго порядка (цилиндр, конус, сфера).

Теорема 1.Если две поверхности 2-го порядка пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой.

На рис. 9.5 показаны фронтальные проекции сферы и цилиндра. Результатом их пересечения являются две кривые второго порядка l и m, а именно – окружности.

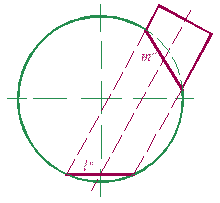
Рис. 9.5

Теорема 2.Если две поверхности 2-го порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания.

На рис. 9.6 изображено пересечение сферы и эллиптического цилиндра (фронтальная и профильная проекции). Точки А и В – точки

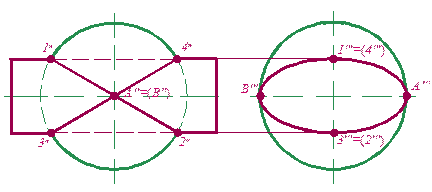
Рис. 9.6

касания поверхностей. Линия пересечения распадается на две кривые второго порядка 1-2 и 3-4 –эллипсы.

Теорема 3.Если две поверхности 2-го порядка описаны около третьей поверхности второго прядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

На рис. 9.7 показано пересечение двух круговых цилиндров одного диаметра – описанных около сферы (фронтальные проекции). Точки А и В – точки касания поверхностей. Линия пересечения распадается на две кривые второго порядка l и m –эллипсы, плоскости которых проходят через прямую, соединяющую точки А и В.

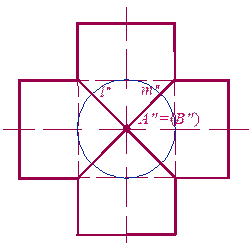
Рис. 9.7