Развертка прямого кругового цилиндра

При построении развертки поверхности прямого круговогоцилиндра можно не прибегать к замене цилиндрической поверхности призматической. Развертка боковой поверхности цилиндра представляет собой прямоугольник, одна сторона которого равна длине окружности πd, а другая - высоте цилиндра.

Рассмотрим пример. На рис. 10.2 а) показан круговой цилиндр, который пересекает фронтально-проецирующая плоскость α_V. Построим развертку усеченного цилиндра.

Разделим цилиндр на 12 равных частей. Чтобы не загромождать чертеж на рис. 10.2 а) обозначена только половина точек 1′…7′ (вторая половина симметрична). Построим их фронтальные проекции. На свободном поле чертежа построим развертку полного цилиндра – прямоугольник с соответствующими сторонами, который также разделим на 12 частей (рис. 10.2 б). На этих прямых, соответствующих образующим цилиндра, отложим их высоты z₁ и т.д. Соединив эти точки плавной кривой по лекалу, получим развертку боковой поверхности усеченного цилиндра. Для того, чтобы изобразить полную развертку, необходимо пристроить нижнее и верхнее основания, предварительно определив их натуральную величину.

Нижнее основание представляет собой круг, его натуральная величина имеется на горизонтальной проекции. Верхнее основание усеченного цилиндра - эллипс. Его натуральную величину можно определить, применив один из способов преобразования чертежа (занятие 5). На чертеже использованспособ перемены плоскостей проекций, в котором дополнительно вводится новая горизонтальная плоскость проекций (рис. 10.2 а).

Таким образом, пристроив основания к развертке боковой поверхности, на чертеже имеем полную развертку усеченного цилиндра (рис. 10.2 б).

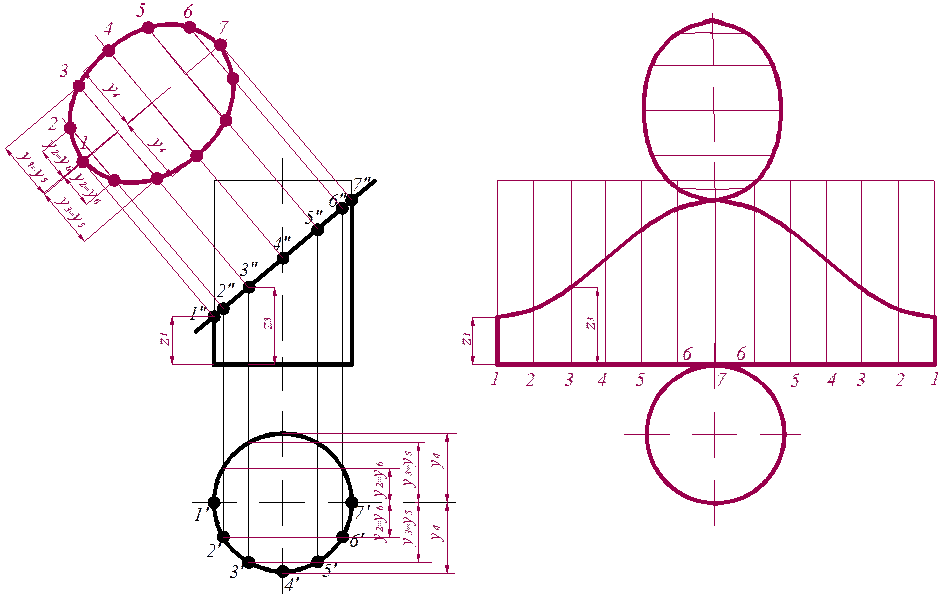
Рис. 10.2