Развертка прямого кругового конуса

Разверткой поверхности прямого круговогоконуса является круговой сектор с углом α, который определяется по формуле

α = d/L • 180,

где d - диаметр окружности основания конуса;

L - длина образующей.

Рассмотрим пример. На рис. 10.3 а) показан круговой конус, который пересекает фронтально-проецирующая плоскость α_V. Построим развертку боковой поверхности усеченного конуса.

Для того чтобы уменьшить количество линий построения и тем самым облегчить понимание чертежа, разделим основание конуса не на 12 равных частей, а на 6. На рисунке обозначена только половина точек - 1′…4′ (вторая половина симметрична). Соединив точки с вершиной, получим образующие. Построим их фронтальные проекции. Затем на горизонтальной проекции строят верхнее основание усеченного конуса – эллипс А2₁С3₁В (занятие 6).

На свободном поле чертежа построим развертку полного конуса – круговой сектор с соответствующим углом α, который также разделим на 6 частей (рис. 10.3 б). На этих прямых, соответствующих образующим поверхности, отложим отрезки длин усеченного конуса, предварительно определив их натуральные величины. На фронтальной проекции имеем истинные размеры только очерковых образующих - n_1-A и n_4-В (рис. 10.3 а). Отрезки образующих 2-2₁ и 3-3₁ вращаем по поверхности конуса (вокруг оси, проходящей через вершину конуса и перпендикулярную плоскости V – занятие 5) до совмещения с очерковыми образующими. Их натуральные величины – n_2-21 и n_3-31. Соединив полученные точки на круговом секторе плавной кривой по лекалу, получим развертку боковой поверхности усеченного цилиндра (рис. 10.3 б).

Для того, чтобы изобразить полную развертку, необходимо пристроить нижнее и верхнее основания, предварительно определив их натуральную величину.

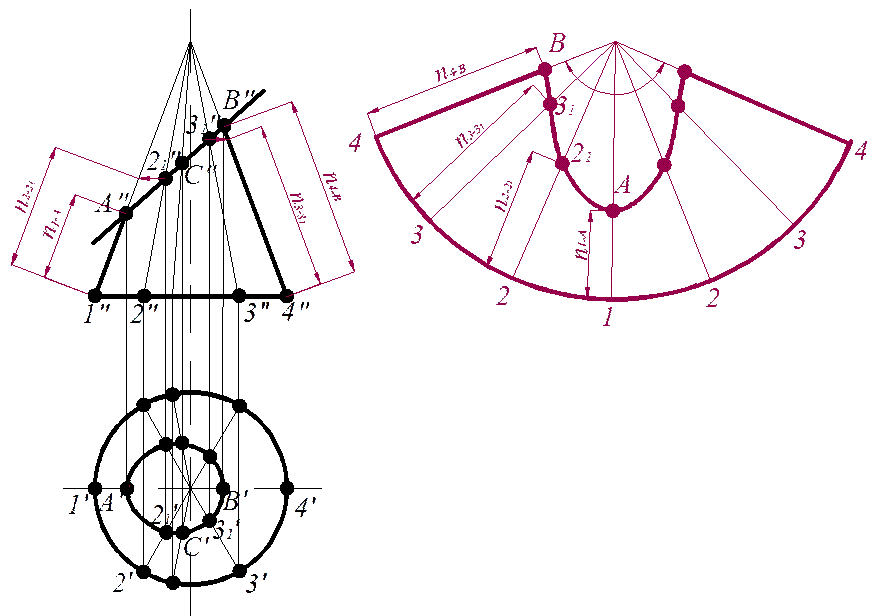
Рис. 10.3