Взаимозаменяемость по форме поверхностей деталей. Обозначения на чертежах.

В основу нормирования и количественной оценки отклонений формы положены понятия прилегающих поверхностей, линий (прямых) и других геометрических элементов, определяющих границу детали.

Когда мы говорим о погрешности на волнистость, на шероховатость и т.д., мы имеем в виду границу поверхности. Номинальная граница поверхности - некоторая часть виртуального пространства, которая отделяет материал детали от окружающей среды. В общем понятие о реальной поверхности становится практически философским, потому что можно помимо шероховатости рассмотреть нано-структуры, оказывается молекулярные, атомные, субатомные структуры и т.д. Деталь постоянно обменивается с окружающей средой своим веществом, как и наоборот, поэтому понятие границы становится таким расплывчатым, но при выполнении технических измерений и решении вопроса о годности или негодности детали пользуются некими моделями, которые в той или иной мере соответствуют реальной границе, т.е. той границе ниже которой находится вещество детали, а выше - окружающая среда.

Под прилегающей прямой к реальному профилю детали понимают прямую, отвечающую следующим условиям:

1. прямая должна хотя бы в одной точке касаться реального профиля, но нигде в пределах нормируемого участка L не пересекать его.

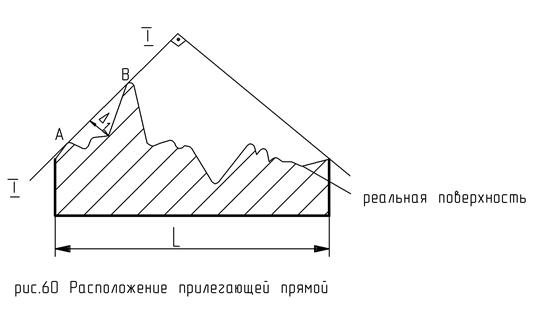
Выполняя первое условие мы с вами можем провести целый ряд прямых, из этих прямых нам нужно выбрать некоторую прямую, которая будет являться прилегающей.

2. Прилегающая прямая должна располагаться относительно профиля так, чтобы расстояние самой удаленной точки профиля до этой прямой было минимальным.

Эту задачу решать с помощью геометрических построений просто. Расстояние от любой точки профиля до прямой измеряется по нормали, опущенной на эту прямую. Профиль остается одним и тем же, а прямая может перемещаться в пространстве произвольно, поскольку сама прямая виртуальна. Для каждой из прямых мы можем создать множество расстояний и выбрать максимальное, т. е. заменим реальную деталь ее прилегающей прямой. Аналогично можно сделать по плоскости.

Для этого мы выделяем нормируемый участок плоскости, располагаем на нем прилегающую плоскость и опять решаем задачу минимакса, только не в одномерной, а в двумерной постановке. В общем случае, это может быть фигурная поверхность. Главное, чтобы прямая, плоскость или какая-то прилегающая поверхность повторяла форму номинальной поверхности.

Максимальное отклонение от точки профиля до прилегающей прямой обозначается Δ, допуск на это отклонение обозначается Т. В основу нормирования (определения годности детали) положено соотношение Δ≤T по всем типам подобных отклонений.

При измерениях в качестве прилегающих геометрических элементов могут служить рабочие поверхности контрольных плит, интерференционных стекол, калибров, оправок и тому подобное.

Рассмотрим конкретные виды отклонений.

Отклонение от плоскостности.

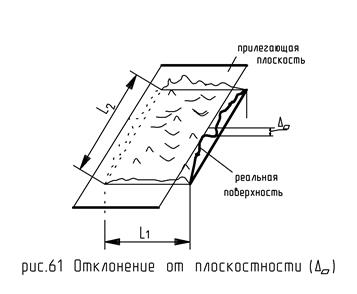
Рассмотрим некоторый элемент поверхности, с нормируемыми участками L₁ и L₂. Необходимо найти прилегающую плоскость, измерить расстояние от нее до реальной поверхности, и определить максимальную величину.

Отклонение от плоскостности обозначается следующим образом: Δ_□

Определили величину максимального отклонения реального профиля от прилегающей плоскости Δ. Теперь надо решить вопрос о годности детали. Для этого мы должны сопоставить величину максимального отклонения с величиной допуска:

Δ_□ ≤ Т_□.

Допуски учитываются только, если они лежат внутри поля общего допуска на размер. Для того, чтобы изобразить поле допуска на плоскостность, мы должны отложить от прилегающей плоскости глубину материала детали, величину допуска и вторую плоскость, которая будет параллельна найденной нами ранее прилегающей плоскости. Верхняя граница поля допуска плоскостности соответствует прилегающей плоскости. Нижняя граница отстоит на величину допуска в глубь материала от верхней границы. Область пространства между этими двумя параллельными плоскостями и называется полем допуска плоскостности.

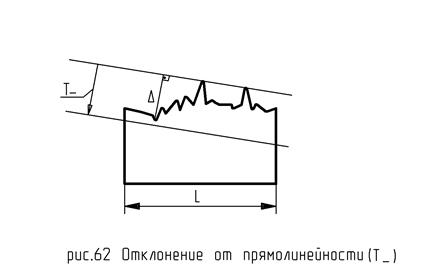
Отклонение от прямолинейности.

Нормируется для профиля детали. Аналогично отклонению от плоскостности (рис. 62).

Δ₋ ≤ Т₋.