Способ триангуляции (треугольников)

Способ применяется для построения развертки пирамидальных поверхностей. Сущность способа: последовательное совмещение всех граней пирамиды, которые представляют собой треугольники, с плоскостью.

Построим развертку поверхности пирамиды (рис 10.1), в основании которого лежит правильный треугольник АВС с вершиной S. Определим натуральную величину ребер. В данном случае SА=SВ=SС. На рис 10.1 показано определение натуральной величины ребра SА с помощью способа вращения его вокруг оси i, перпендикулярной плоскости V. Таким образом, натуральная величина ребер равна S′А₁′. Поскольку основание пирамиды параллельно плоскости Н, то его натуральная величина есть А′В′С′.

Приступим к построению развертки. Для этого из произвольной точки S₀ проводят произвольную прямую и откладывают на ней величину ребра пирамиды S₀А₀ = S′А₁′. Из точки S₀ проводят дугу радиусом r = AB= А′B′, а из S₀ – дугу R = SB = SA = S′А₁′. Пересечение дуг укажет положение B₀. Аналогично находятся точки С₀ и А₀. Соединив полученные точки S₀А₀B₀С₀А₀, получим развертку боковой поверхности пирамиды. Чтобы получить полную развертку поверхности, достроим основание А₀B₀С₀ = А′В′С′.

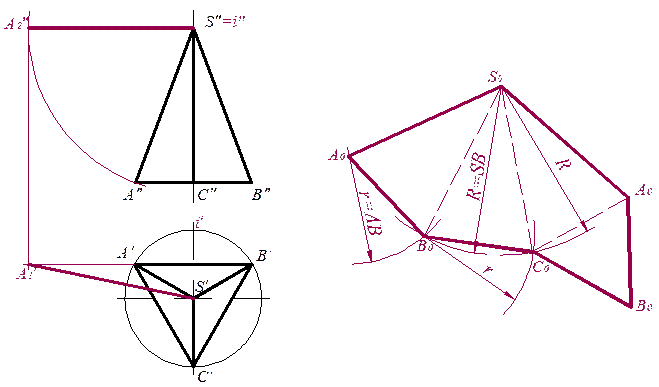
Рис. 10.1

Способ нормального сечения

Способ применяется для построения развертки призматических поверхностей при условии, если ребра призмы, параллельны какой-либо плоскости проекций. Если ребра занимают произвольное положение, то перед построением развертки следует преобразовать чертеж.

При способе нормального сечения алгоритм построения развертки следующий:

1. пересечь призматическую поверхность вспомогательной плоскостью, перпендикулярной к ее ребрам, в результате чего получится некоторое сечение;

2. определить натуральную величину полученного сечения;

3. в произвольном месте чертежа провести произвольную прямую, на которой отложить отрезки, конгруентные сторонам сечения;

4. провести перпендикуляры, соответствующие ребрам призмы и на них отложить их натуральную величину.

Способ раскатки

Способ применяется для построения развертки призмы в том случае, если основание призмы параллельно какой-либо плоскости проекций, а ее ребра параллельны другой плоскости проекций.

Сущность способа.За плоскость развертки принимается плоскость β, проходящую через одно из ребер призмы, и параллельную одной из плоскостей проекций. Далее последовательно совмещаются грани с плоскостью β путем их поворота вокруг выбранного ребра.