СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСИ,

ПЕРПЕНДИКУЛЯРНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ

Сущность метода: плоскости проекций остаются неподвижными, а геометрический объект меняет свое положение. При вращении каждая точка геометрической фигуры перемещается в плоскости, перпендикулярной к оси вращения. Траектория движения точек представляет собой окружность.

Решение четырех основных задач методом вращения вокруг оси, перпендикулярной плоскости проекций:

Задача 1.

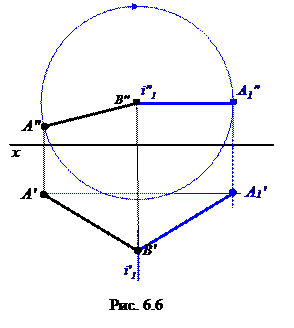На рис. 6.6 задан отрезок общего положения АВ. Обозначим i₁ - ось вращения. Пусть i₁ ^ V и проходит через точку В. Тогда при вращении вокруг оси В останется на месте, А будет перемещаться в плоскости, перпендикулярной i₁, а следовательно параллельной V. Таким образом, окружность, по которой движется точка, на плоскость V проецируется без искажения, а на плоскость Н – в отрезок, параллельный оси х.

Для того, чтобы отрезок АВ занял положение уровня, переместим А по окружности так, чтобы В″А₁″ ║ х. Положение А₁′ будет находится на пересечении линии связи, проведенной от А₁″ и горизонтальной прямой от А′ (проекции окружности).

Таким образом, отрезок АВ занял положение горизонтали (А₁″В″ - натуральная величина АВ, угол между А₁′В′ и х является действительной величиной угла наклона АВ к плоскости V).

Задача 2.

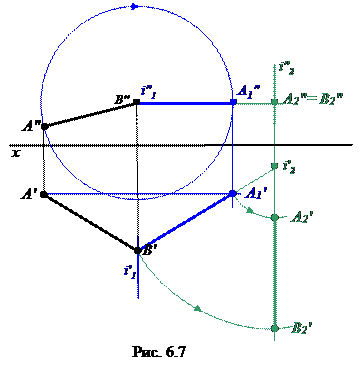На рис. 6.7 задан отрезок общего положения АВ. Для того, чтобы АВ занял проецирующее положение, его сначала нужно перевести в положение уровня. Выполнив для этого необходимые действия (см. задачу 1), введем еще одну ось вращения i₂ ^ Н. Переместим А₁′ и В′ по окружности так, чтобы А₂′ В₂′ ^ х. Положение А₂″ и В₂″ будет находится на пересечении линии связи, проведенной от А₂′ В₂′ и горизонтальной прямой от В″А₁″ (проекции окружности, по которой двигались А₁′ и В′).

Таким образом, отрезок АВ занял фронтально-проецирующее положение.

Задача 3.

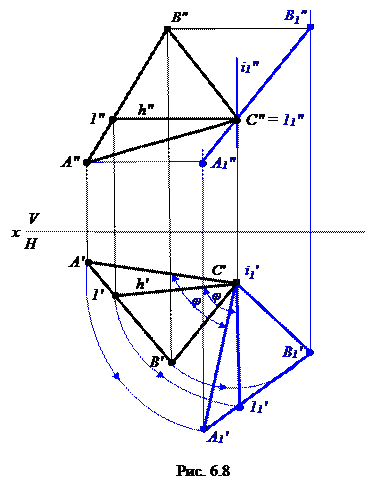
На рис. 6.8 задана плоскость общего положения АВС. Для того чтобы она заняла проецирующее положение, зададим какую-либо линию уровня плоскости, например горизонталь плоскости h. Пусть ось вращения i₁ ^ Н и проходит через точку С. Переведем h во фронтально-проецирующее положение путем вращения вокруг оси i₁. При этом она повернется на угол φ. На такой же угол вращают остальные точки плоскости А, В, С. Таким образом, получим фронтально-проецируюшую плоскость А₁В₁С (угол между В₁″С″А₁″ и х является действительной величиной угла наклона АВС к плоскости Н).

Задача 4.

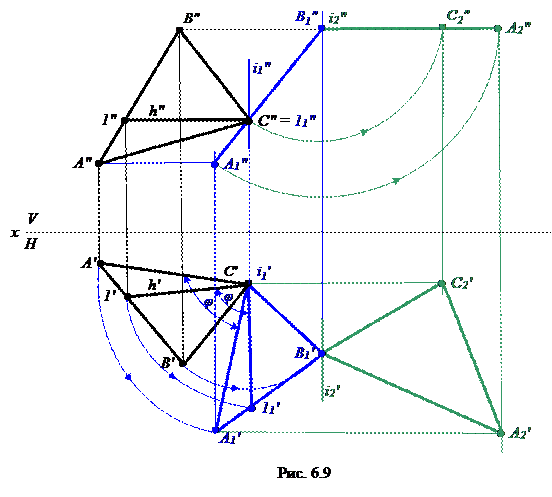
На рис. 6.9 задана плоскость общего положения АВС. Для того чтобы она заняла положение плоскости уровня, ее сначала нужно перевести в проецирующее положение. Выполнив для этого необходимые действия (см. задачу 3), введем еще одну ось вращения i₂ ^ V, которая проходит через точку В. Провращаем плоскость А₁В₁С так, чтобы А₂″В₁″С₂″ ║ x. Таким образом, плоскость займет положение горизонтальной плоскости (А₂′В₁′С₂′ - натуральная величина АВС).

КРИВЫЕ ЛИНИИ

Кривую линию можно представить как траекторию точки, перемещающейся в пространстве или на плоскости,

Кривые линии могут быть плоские, т.е. такие, все точки которых принадлежат одной плоскости и пространственные, точки которых не принадлежат одной плоскости.

Примерами плоских кривых являются: окружность, эллипс, парабола. Примером пространственной кривой является винтовая линия.

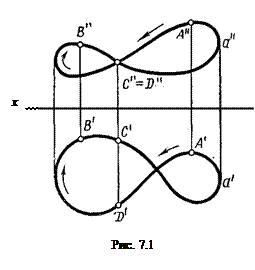Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить их между собой в той же последовательности, в какой они располагались на оригинале (рис.7.1.).

ПОВЕРХНОСТИ