ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ МЕТОДОМ СЕКУЩИХ ПЛОСКОСТЕЙ

Рассмотрим применение данного метода на примере построения линии пересечения полусферы с прямым круговым конусом (рис. 9.1).

В качестве вспомогательных секущих плоскостей удобно использовать несколько горизонтальных плоскостей (на рис. 9.2 – фронтальные следы плоскостей a_V и β_V), т.к. в пересечении таких плоскостей с каждой заданной поверхностью (полусферой и конусом) получатся простые линии – окружности.

Построение начинают с отыскания характерных точек. 1″, 2″, 3″ - проекции самой высокой и низких точек, т.к. являются точками пересечения фронтальных проекций

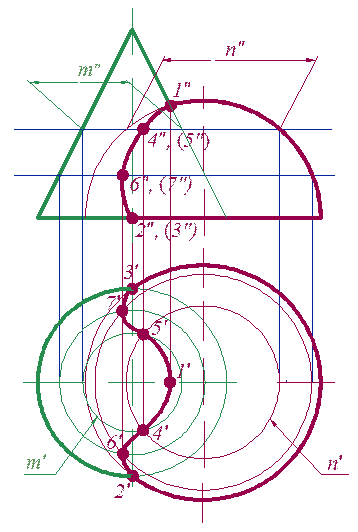
очерков, а центр полусферы и ось конуса лежат в плоскости, параллельной плоскости V. Проекцию самой высокой точки 1′ находят, как принадлежащую очерковым образующим поверхностям. Проекции самых низких точек 2′ и 3′ строят по условию принадлежности основаниям полусферы и конуса.

Теперь обе поверхности пересечем секущими плоскостями, расположенными между точками 1 и 2, 3.

Плоскость a пересекает поверхности по окружностям n и m. Точки пересечения этих окружностей n ∩ m = 4, 5. 4 и 5 принадлежат одновременно и полусфере и конусу, а следовательно и принадлежат линии пересечения этих поверхностей.

Проведя аналогичные действия с плоскостью β, получим точки 6 и 7.

Соединим построенные точки плавной линией с помощью лекала.