Взаимосвязь систем счисления используемых в вычислительной технике.
Двоичная система счисления, используемая элементами вычислительной техники имеет один недостаток – это громоздкость записи. Для того, чтобы записать число 255(10) требуется целых восемь разрядов 11111111(2). Для уменьшения разрядности при записи информации требовалось разработать системы счисления, в которые было бы легко переводить информацию из двоичной системы счисления, и при этом запись была бы менее громоздкой. Сначала была разработана восьмеричная система счисления, в которой тоже самое число 255(10) представлялось в виде 377(8), а затем шестнадцатеричная, это же число в которой имеет вид FF(16). Перевод между этими системами счисления можно осуществлять при помощи таблицы 2.
Таблица 2.
| Двоичная | Восьмеричная | Шестнадцатеричная |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
Перевод из одной системы счисления в другую.
Существует три способа перевода чисел из одной системы счисления в другую, это:
1. Перевод с использованием формулы разложения по степени основания;
2. Перевод целых чисел делением на основание;
3. Поразрядные способы перевода (переводы с использованием таблиц).
Перевод с использованием формулы разложения по степени основания.
В основе способа перевода лежит использование веса разрядов чисел. Перевод с использованием формулы разложения по степеням основания удобен для перевода в десятичную систему счисления, так как в процессе преобразования действия выполняются в новой системе счисления.
Алгоритм перевода из одной системы счисления в другую представлен на рисунке 7.
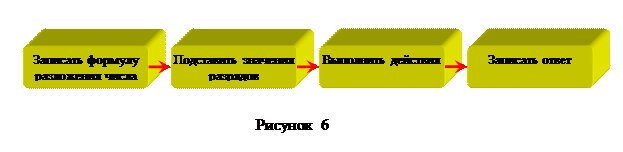
Рассмотрим процесс перевода с использованием формулы разложения по степени основания на примерах:
Пример 1.
Дано A(2)=10011. Найти A(10). Решение примера приведено на рисунке 7.
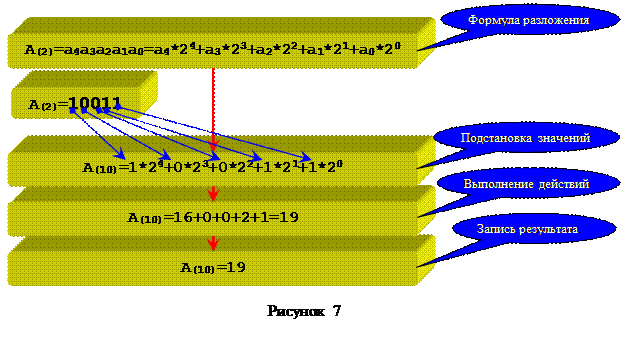
Пример 2.
Дано A(8)=257. Найти A(10).
Решение:
A(8)= a2a1a0=a2*82+a1*81+a0*80
A(10)= 2*64+5*8+7*1=128+40+7
A(10)=175
Пример 3.
Дано A(16)=1EF6. Найти A(10).
Решение:
A(16)= a3a2a1a0= a3*163+a2*162+a1*161+a0*160
A(10)= 1*4096+14*256+15*16+6*1=4096+3584+240+6
A(10)=7926
Дата добавления: 2016-11-04; просмотров: 2450;











