Поразрядные способы перевода.
Перевод чисел упрощается, если основание старой системы счисления p и новой системы счисления q связаны отношением:
p=qk или q=pk,
где:
p – основание исходной системы счисления;
q – основание результирующей системы счисления;
k – целое число.
Для систем счисления используемых в вычислительной технике значение k приведено в таблице 3.
Таблица 3.
| Исходная система счисления | Результирующая система счисления | Значение k |
| Восьмеричная | Двоичная | |
| Двоичная | Восьмеричная | |
| Шестнадцатеричная | Двоичная | |
| Двоичная | Шестнадцатеричная |
При такой связи систем счисление перевод осуществляется с помощью таблиц 4 и 5.
Таблица 4.
Взаимосвязь восьмеричной и двоичной систем счисления.
| Двоичная | Восьмеричная |
Таблица 5.
Взаимосвязь шестнадцатеричной и двоичной систем счисления.
| Шестнадцатеричная | Восьмеричная |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Алгоритм поразрядного перевода из двоичной системы счисления в восьмеричную заключается в дроблении двоичного числа по три разряда с права на лево и замене соответствующими цифрами восьмеричной системы счисления из таблицы 4. Если в конце дробления остается меньше трех разрядов, то двоичное число дополняют с лева нулями. Алгоритм перевода представлен на рисунке 8.
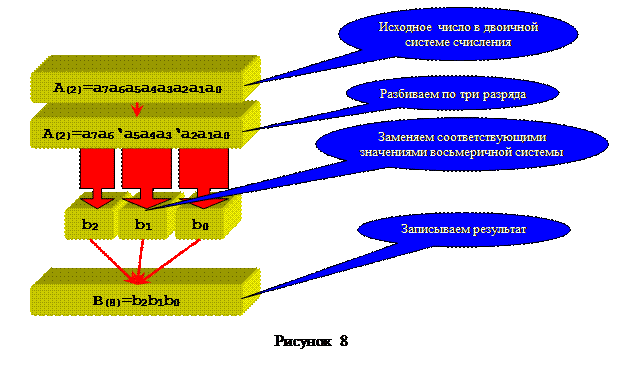
Обратный перевод из восьмеричной в двоичную систему счисления осуществляется по этому же алгоритму но в обратном порядке. Один разряд восьмеричной системы счисления заменяется тремя разрядами двоичной систем счисления.
Алгоритм перевода из двоичной в шестнадцатеричную систему счисления аналогичен алгоритму перевода в восьмеричную, за исключением того, что число дробиться не по три, а по четыре разряда и соответствия подбираются из таблицы 5.
Пример 1.
Дано A(2)=1001101. Найти A(8).
Решение:
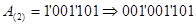
Ответ:
A(8)=115
Пример 2.
Дано A(8)=27. Найти A(2).
Решение:
A(8)=2’7
Ответ:
A(2)=010111=10111
Пример 3.
Дано A(2)=1101101. Найти A(16).
Решение:
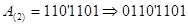
Ответ:
A(16)=6D
Пример 2.
Дано A(16)=F4. Найти A(2).
Решение:
A(16)=F’4
Ответ:
A(2)=11110100
Дата добавления: 2016-11-04; просмотров: 2392;











