Интервал между двумя событиями. Абсолютность интервала

Рассмотрим воображаемое четырехмерное пространство, на осях отложим три пространственные координаты и время. Любое событие в этом пространстве изображается точкой, называемой мировой точкой. При движении частицы изображается мировая линия в четырехмерном пространстве. Прямая мировая линия соответствует равномерному и прямолинейному движению частицы.

Рассмотрим первое событие в системе K – сигнал отправляется в момент времени 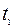из точки с координатами 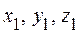. Второе событие в системе K состоит в том, что сигнал приходит в точку с координатами 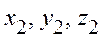в момент времени t₂. Сигнал распространяется со скоростью света c, поэтому он пройдет расстояние 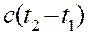. Это расстояние можно также записать в виде:

.

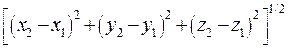Возведем в квадрат расстояния и приравняем их

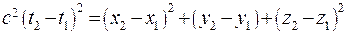(18.10)

Получим зависимость между координатами и временем в системе K

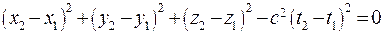(18.11)

В системе K' также получим

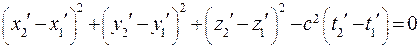(18.12)

Интервалом между любыми событиями называется величина

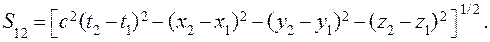(18.13)

Если интервал S₁₂ равен нулю в одной системе, то он будет равен нулю и в другой системе. Интервал является абсолютной величиной, т.к. он инвариантен по отношению к преобразованию от одной инерциальной системы отсчета к другой. Эта инвариантность является следствием постоянства скорости света.

Введем обозначения

, .

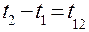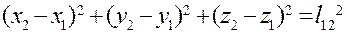Тогда

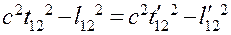(18.14)

Рассмотрим, какие события возможны. Пусть в системе K' два события произошли в одной точке, тогда

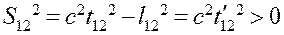(18.15)

Отсюда следует, что интервал между событиями должен быть вещественным, он называется времениподобным.

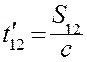(18.16)

Если два события происходят с одним и тем же телом, то интервал всегда является времениподобным.

Пусть теперь два события произошли в системе K' в одно и то же время, т.е. 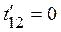, тогда

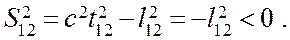(18.17)

Интервал между этими событиями мнимый, такой интервал называется пространственноподобным.

Рассмотрим для простоты пространство с одной осью координат x и осью времени t. Пусть мировая точка будет началом координат. Прямолинейное равномерное движение, проходящее через точку x= 0 при t = 0 изобразим прямой линией, наклоненной к оси t под углом, тангенс которого равен скорости света. На рис. 18.2 изображены две прямые, соответствующие распространению двух сигналов со скоростью света в противоположных направлениях, на этих прямых 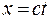. Линии, изображающие движение частиц могут лежать только внутри областей aOc и dOb, в этих областях 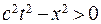, т.е. интервалы времениподобные. Все события области aOc являются будущими по отношению к О, т.е. не допускается, чтобы какое-нибудь событие области aOc происходило раньше события О.

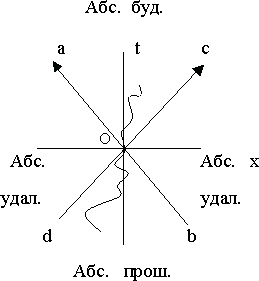
Рис. 18.2.

События области dOb называются абсолютно прошедшими, а события области aOc – абсолютно будущими по отношению к О, в этих областях интервал между событиями называется времениподобным ( 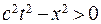). Интервал между событиями в областях aOd и cOb - пространственноподобный ( 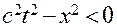). В любой системе отсчета эти события не могут произойти в одном месте. Эти области называются абсолютно удаленными по отношению к О. Всегда можно выбрать такую систему, где события происходят раньше, позже или одновременно. Если рассматривать все три пространственные координаты, то области aOc и dOb изображаются внутри светового конуса.