Принцип наименьшего действия Гамильтона

Для любой механической системы существует функция S, называемая действием, которая для реального движения должна принимать наименьшее (или наибольшее) значение. Следовательно, вариация действия 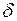S = 0. Для свободной частицы, перемещающейся вдоль некоторой мировой линии из точки q₁ в точку q₂ (рис.19.1) действие имеет вид

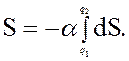(19.1)

где dS - элементарный интервал,

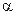- постоянная, характеризующая данную частицу.

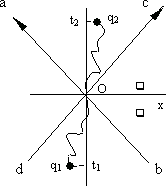
Рис.19.1.

Действие можно представить как интеграл по времени

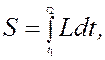(19.2)

где 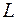- функция Лагранжа для данной механической системы.

Поскольку 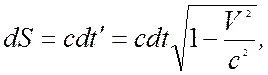находим

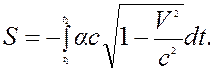(19.3)

Отсюда получим функцию Лагранжа для частицы

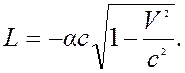(19.4)

Поскольку функция Лагранжа в классической механике

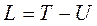, (19.5)

где T - кинетическая энергия;

U - потенциальная энергия;

то в предельном случае c 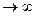функция Лагранжа должна принимать значение

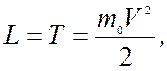(19.6)

т.к. для свободной частицы U = 0.

Разложим функцию Лагранжа в ряд по V/c:

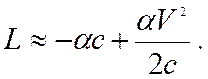(19.7)

Постоянную 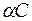можно опустить, т.к. функция Лагранжа, как и энергия, определяется с точностью до постоянной:

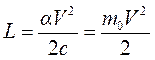, (19.8)

отсюда получим

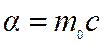. (19.9)

Таким образом, для свободной материальной точки функция Лагранжа

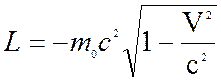. (19.10)

Импульс частицы

Импульсом частицы называется вектор

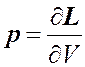. (19.11)

Подставим (10.10) в (10.11), находим

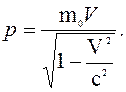(19.12)

В предельном переходе c

.

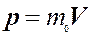Сила

Силой называется производная от импульса по времени:

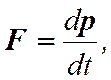или запишем в виде

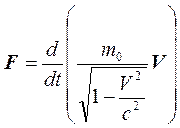. (19.13)

Это основное уравнение релятивистской динамики.

Если скорость частицы изменяется только по направлению, т.е. сила перпендикулярна к скорости, то она имеет вид

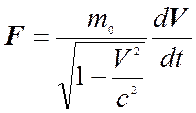(19.14)

где m₀ - масса покоя частицы.

Если же скорость изменяется только по величине, т.е. сила направлена по скорости

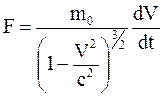. (19.15)

Отсюда видно, что отношение силы к ускорению различно в этих случаях. Это означает, что выражение для силы в общем случае должно включать оба этих выражения (10.14) и (10.15).

Энергия

Энергией частицы называется величина

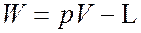. (9.16)

Подставим в (10.16) импульс p и функцию Лагранжа L, получим

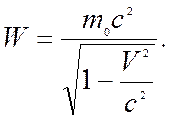(19.17)

Если скорость частицы обращается в нуль, то ее энергия называется энергией покоя

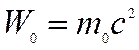. (19.18)

При малой скорости V<< c

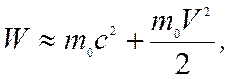, (19.19)

что, без учета постоянной 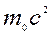, дает классическое выражение для кинетической энергии.

Эйнштейн записал связь между энергией и массой частицы в виде

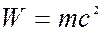, (19.20)

где 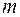- релятивистская масса.

Отсюда следует, что нет необходимости вводить выражение для массы

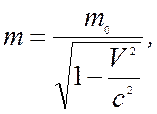(19.21)

т.к. масса и энергия пропорциональны:

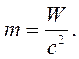(19.22)

В связи с этим, нет необходимости говорить о законах сохранения энергии и полной массы, т.к. это эквивалентные понятия.