Электроемкость плоского конденсатора

Напряженность электрического поля внутри конденсатора одинакова во всех его точках и связана с напряжением между его обкладками соотношением

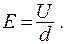(15.13)

Поверхностная плотность заряда на обкладках конденсатора:

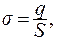(15.14)

где S - площадь пластины.

Напряженность поля между обкладками:

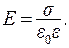(15.15)

Найдем электроемкость плоского конденсатора:

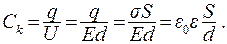(15.16)

Емкость плоского конденсатора пропорциональна площади обкладок S и обратно пропорциональна расстоянию между обкладками d:

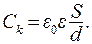(15.17)

Напряженность электрического поля в конденсаторе уменьшается, если внутри конденсатора помещен диэлектрик. Для каждого диэлектрика существует напряжение пробоя 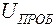, выше которого происходит разрушение диэлектрика:

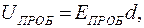(15.18)

где 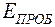- напряженность, при которой происходит пробой диэлектрика. Параллельное соединение конденсаторов служит для увеличения емкости батареи без сильного увеличения ее размеров (рис. 15.4).

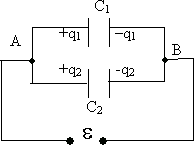
Рис. 15.4.

Разность потенциалов между точками А и В одинакова для конденсаторов. Заряды на конденсаторах:

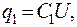
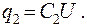(15.19)

Полный заряд

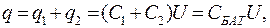(15.20)

отсюда емкость батареи при параллельном соединении конденсаторов равна сумме емкостей отдельных конденсаторов:

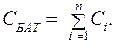(15.21)

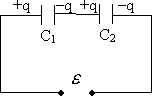
Рис. 15.5.

Последовательное соединение конденсаторов служит для предотвращения пробоя системы (рис. 15.5). Вследствие электростатической индукции на всех пластинах будут одинаковые по величине и противоположные по знаку заряды + q и – q.

Разность потенциалов на каждом из конденсаторов:

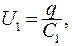
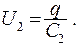(15.22)

Полное напряжение U равно сумме напряжений на отдельных конденсаторах:

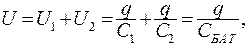(15.23)

отсюда следует, что величина, обратная к электроемкости батареи, равна сумме обратных электроемкостей отдельных конденсаторов:

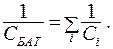(15.24)