Электроемкость сферического проводника

Напряженность проводника вне его поверхности (r > R) равна по величине и по направлению напряженности точечного заряда, помещенного в центр сферического проводника:

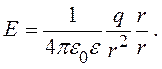(15.6)

Потенциал электрического поля вне сферического проводника (r > R):

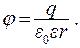(15.7)

На поверхностисферы (r = R):

(15.8)

отсюда находим

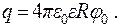(15.9)

Электроемкость сферического проводника:

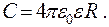(15.10)

Если принять Землю за шар радиусом R = 6400 км, находящийся в среде с диэлектрической проницаемостью ε = 1, то электроемкость Земли: 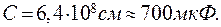При заземлении заряженного проводника, его заряд равномерно перераспределяется по всей поверхности проводника и Земли. Поскольку размер проводника 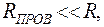то и 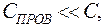поэтому заряд, который останется на проводнике, будет много меньше, чем первоначальный.

Электроемкость уединенного проводника зависит от его размеров, формы, диэлектрической проницаемости среды, и не зависит от величины заряда проводника.

Конденсаторы

Емкость проводника изменяется, если вблизи него находятся проводящие тела. Пусть одна пластина заряжена положительно, тогда, вследствие электростатической индукции, другая пластина, находящаяся на расстоянии d, будет заряжена отрицательно.

Если принять потенциал одной пластины j₁ = j, а потенциал другой пластины j₂ = 0 отсюда 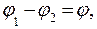тогда емкость второй пластины

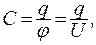(15.11)

где 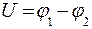- разность потенциалов между двумя пластинами.

Емкость конденсатора, представляющего собой систему из двух проводников:

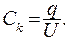(15.12)

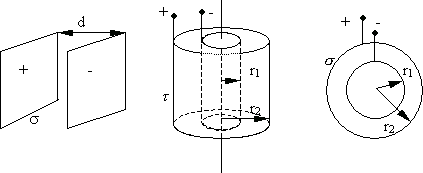
Рис. 15.3.

Конденсаторы могут иметь различную форму: плоскую, цилиндрическую, сферическую (рис. 15.3). Между обкладками конденсатора помещают диэлектрик, который повышает электроемкость конденсатора.