Вычерчивание плоского контура детали с выполнением сопряжений (графическая работа)

Задание:

Построить изображение плоского контура детали с выполнением сопряжений на формате А4 (формат располагается вертикально). Масштаб – 1:2. Исходные данные приведены ниже. Линии построения не стирать.

Цель работы: Изучение типов линий и приобретение навыков их выполнения (ГОСТ 2.303-68). Изучение построений сопряжений в очертаниях технических форм. Ознакомление с основными правилами нанесения размеров (ГОСТ 2.307-68). Изучение приемов написания букв и цифр чертежным шрифтом (ГОСТ 2.304-81). Применение масштаба.

Методика оформления и последовательность выполнения задания "Очертания технических форм":

1. Подготовить формат А4. Нанести внутреннюю рамку и прямоугольник основной надписи.
2. По размерам, нанесенным на исходные данные, установить габариты изображения и спланировать габаритный прямоугольник на чертеже так, чтобы очерк детали расположился примерно в середине поля формата.
3. Выбрать базовые линии очерка детали и нанести их на чертеже. Вычертить в тонких линиях контур детали, проведя все вспомогательные построения для центров и точек сопряжения линий.
4. Нанести выносные и размерные линии (ГОСТ 2.307-68). Особое внимание следует обратить на расположение размерных чисел над размерными линиями.
5. Сделать обводку чертежа.
6. Заполнить основную надпись чертежным шрифтом.

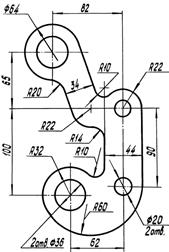
Вар. №	Контур детали	Вар. №	Контур детали

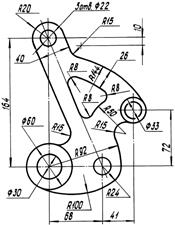
Лекальные кривые

Все множество плоских кривых можно разделить на циркульные и лекальные. Циркульной называют кривую, которую можно построить с помощью циркуля. К ним относятся окружность, овал и т.д.

Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.

Лекальные кривые можно разделить на закономерные и незакономерные.

Закономерными называют кривые, которые можно задать алгебраическим выражением. Незакономерные кривые нельзя задать алгебраическим выражением.

Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.

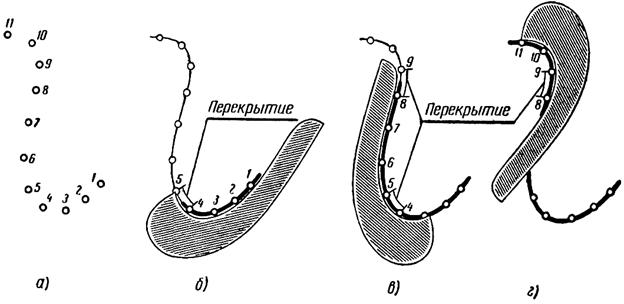
Лекальная кривая – это плавная кривая линия.Лекальную кривую нельзя даже частично провести с помощью циркуля. Лекальные кривые чертят с помощью лекал.

Рассмотрим построение лекальных кривых на примере Эллипса и Спирали Архимеда.

Эллипс– это замкнутая кривая. Его большая и малая оси есть оси симметрии эллипса. Точки F1 и F2 - это фокусы эллипса. Сумма расстояний от любой точки эллипса (от М, от N, ...) до фокусов F1 и F2 есть величина постоянная. Она равна большой оси АВ. Например, F1M + F2M. = AB; F1N + F2>N=AB (рис. 17). Пример построения эллипса приведен на рис.2.

.

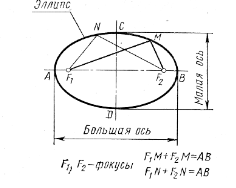
Рис. 1. Лекальная кривая – эллипс

Задание: Выполнить чертеж лекальных кривых (эллипс, спираль Архимеда) на формате А4. Размеры даны в задачах (см. ниже). Название работы: Лекальные кривые.

Задача 1:

Построение лекальной кривой – эллипса

1.Даны большая ось АВ и малая ось CD эллипса

2. Проводим из центра О окружность радиуса ОА и окружность радиуса ОС.

3. Делим большую окружность на 12 равных частей. Точки деления 1, 2, 3, 12 окружности соединяем с центром О. Прямые 1-7, 2-8 ... 6-12 делят малую окружность тоже на 12 равных частей.4. Из точек деления большой окружности проводим прямые параллельные CD. Из точек деления малой окружности проводим прямые, параллельные АВ. Точки пересечения вертикальных и горизонтальных прямых – это искомые точки эллипса. 5. Соединяем точки плавной кривой с помощью лекал (рис.2.).

Примечание: для выполнения данной задачи взять исходные данные: АB=70, СD=40, окружность разделить на 24 части.

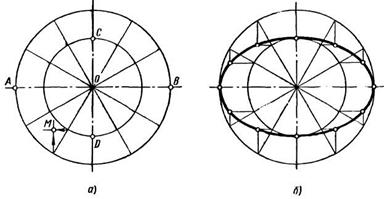
Рис. 2. Построение лекальной кривой – эллипса

Спиралью Архимеда называется плоская кривая, полученная как след точки, движущейся равномерно поступательно от неподвижной точки О по выходящему из нее и равномерно вращающемуся вокруг точки О лучу (радиусу)Точка О называется полюсом спирали; отрезок ОА называется шагом t спирали; отрезок KL – нормалью спирали, а прямая MN, перпендикулярная к нормали, называется касательной; точка К может находиться в любом месте спирали, а точку L находят путем построения, для чего точку К соединяют прямой с точкой О и в точке О проводят перпендикуляр к отрезку КО, который пересечет в точке L окружность, проведенную из центра О диаметром D = t/3,14.

Задача 2:

Построение Архимедовой спирали

Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей. Из конца О отрезка / проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.

На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т.д.

После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую – спираль Архимеда.

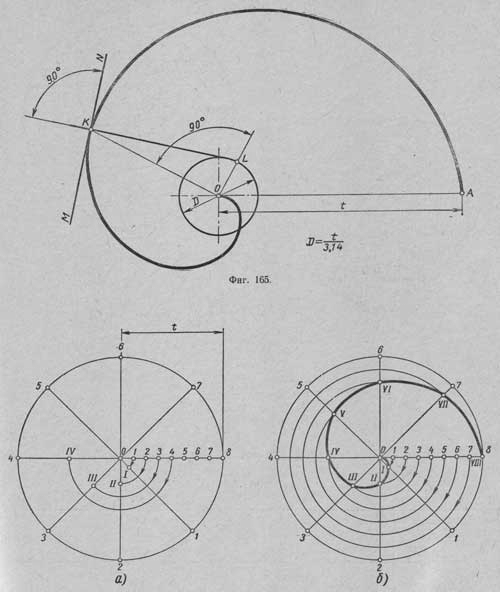
Примечание: для выполнения задания на формате А4 взять следующие значения: R=t=55, окружность разделить на 12 частей.

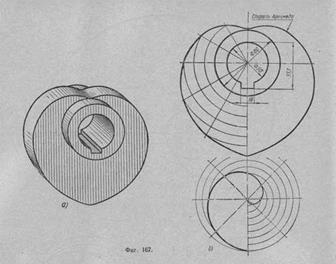
На рисунке дано изображение распределительного кулачка. Очертания боковых сторон его выполняют по спирали Архимеда.

Уклон и конусность

Уклоны. ГОСТ 8908-81

Уклон–это величина, характеризующая наклон одной линии (плоскости) по отношению к другой, i = tg a = ВС/АВ.

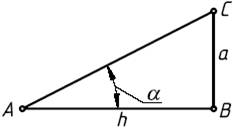
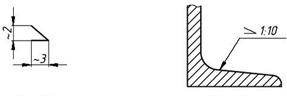Для обозначения уклонов на чертеже применяется знак (рис1) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, острый угол знака должен быть направлен в сторону уклона (рис 2)

Построение уклона. На примере (рисунок) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

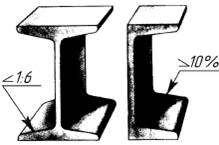
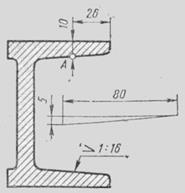
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.