Исследование индуктивной катушки и конденсатора

Индуктивная катушка и конденсатор относятся к реактивным элементам. Протекающий по ним переменный ток вызывает возникновение магнитного и электрического полей соответственно, что сопровождается обратимыми преобразованиями электроэнергии в энергию магнитного или электрического полей. Энергия электрической цепи, вовлечённая в этот процесс, называется реактивной. Реактивная энергия циркулирует между реактивным элементом и источником. В этом заключается основное отличие реактивных элементов от активного (резистора), на котором происходит необратимый процесс преобразования электроэнергии в тепловую, рассеиваемую в окружающей среде. Энергия электрической цепи, участвующая в данном процессе, называется активной. При этом на реактивных элементах наблюдается фазовый сдвиг между синусоидами тока и напряжения, в то время как на активном элементе угол между током и напряжением нулевой.

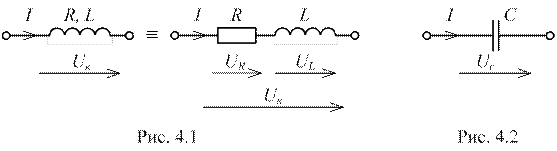
В настоящей работе исследуются индуктивная катушка с постоянными параметрами R, L (рис. 4.1) и конденсатор переменной ёмкости C (рис. 4.2).

Индуктивная катушка представляет собой проводник, намотанный на сердечник. Сердечники обычно выполняются в виде стержня или тора из специальных материалов, предназначенных для концентрации в себе магнитного потока, возникающего при протекании тока по виткам проводника.

В связи со своим конструктивным исполнением индуктивная катушка характеризуется двумя параметрами: а) активным сопротивлением R, представляющим собой активное сопротивление проводника, из которого выполняются витки, б) индуктивностью L, характеризующей основное свойство катушки – создание магнитного поля. В результате этого индуктивная катушка представляется в виде схемы замещения, состоящей из последовательного соединения идеального резистивного элемента с сопротивлением R, равным активному сопротивлению проводника катушки, и идеального индуктивного элемента с индуктивностью L, равной индуктивности катушки (рис. 4.1).

Полное сопротивление катушки записывается через ток и напряжение на ней по закону Ома:

,

где: U_к и I – действующие значения напряжения и тока катушки (под действующим значением тока понимают значение периодического тока, равное такому значению постоянного тока, который за время одного периода производит тот же самый тепловой или электродинамический эффект, что и периодический ток).

На схеме замещения катушка рассматривается как последовательное соединение R и L элементов, поэтому общее сопротивление катушки должно являться суммой сопротивлений этих элементов. Однако, поскольку сопротивления R и L элементов обусловлены различными факторами (электрическим сопротивлением металла и ЭДС самоиндукции соответственно), вводят понятие комплексного сопротивления (представляют общее сопротивление R и L элементов в виде комплексного числа) и рассматривают активное сопротивление R в качестве вещественной части данного комплексного сопротивления, а индуктивное сопротивление X_L, вызываемое индуктивностью L, – в качестве мнимой части: . Благодаря этому R и X_L откладываются по различным осям на комплексной плоскости и поэтому не складываются в одно целое подобно скалярным величинам, а их сумма находится как модуль комплексного числа, т. е. как векторная сумма. Таким образом, полное сопротивление индуктивной катушки связано с параметрами её схемы замещения следующим образом:

,

где: R, – активная и индуктивная составляющие сопротивления соответственно, ω=2∙π·f – угловая частота тока, f – частота тока в цепи.

В связи с вышесказанным, полное сопротивление катушки представляется как гипотенуза прямоугольного треугольника сопротивлений (рис. 4.3), один катет, которого равен R, а другой – X_L. Из треугольника сопротивлений вытекают следующие зависимости:

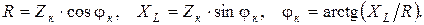
Напряжение на катушке (рис. 4.1), находится (аналогично полному сопротивлению) векторной суммой напряжений последовательно соединённых элементов: 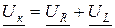. Вектор активной составляющей полного напряжения катушки совпадает по направлению с вектором тока , а вектор реактивной составляющей – опережает вектор тока на угол 90°. Обычно вектор тока в последовательной цепи и совпадающий с ним по фазе вектор при построении векторной диаграммы на комплексной плоскости, откладывают по действительной оси, а вектор – в положительном направлении мнимой оси (так как он опережает вектор тока на угол φ_к= +90°>0). В связи с этим индуктивное сопротивление, обуславливающее индуктивное напряжение, в комплексном виде записывают как . Действующие значения напряжений U_к, U_R, U_L, тока I и соответствующие сопротивления катушки связаны следующими зависимостями:

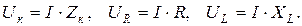
Вектор полного напряжения на индуктивной катушке 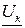опережает вектор тока 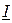на угол φ_к (0°<φ_к<90°). Векторная диаграмма тока и напряжений на индуктивной катушке приведена на рисунке 4.4.

Векторы напряжений , и образуют прямоугольный треугольник напряжений, подобный треугольнику сопротивлений. Из треугольника напряжений получаются следующие зависимости:

Полная мощность катушки S_к по определению равна произведению тока катушки I и напряжения на катушке U_к, т. е.

.

Полная мощность S_к связана с активной Р и реактивной Q_L мощностями индуктивной катушки выражением

.

Активная мощность P численно равна электрической энергии, преобразующейся на катушке в теплоту за единицу времени, и определяется как

.

Реактивная мощность Q_L численно равна мгновенной мощности, находящейся в процессе обмена между магнитным полем катушки и источником электрической энергии. Величина реактивной мощности определяется зависимостью

.

Графически связь между S_к, P и Q_L можно представить в виде прямоугольного треугольника мощностей (рис. 4.5), гипотенуза которого равна S_к, а катеты – P и Q_L. Треугольник мощностей подобен треугольникам сопротивлений и напряжений. Из него вытекают следующие соотношения:

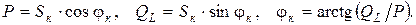
Величина соs(φ) называется коэффициентом мощности. Данный коэффициент показывает какую часть от полной мощности S составляет активная мощность P (из треугольника мощностей cos(φ)=P/S).

Конденсатор представляет собой обкладки, разделённые диэлектриком. Данная конструкция способствует возникновению электрического поля между обкладками, на которых скапливаются разноимённые электрические заряды.

В любом диэлектрике, разделяющем заряженные обкладки конденсатора, будут возникать токи утечки за счёт проникновения зарядов сквозь него. Однако данные токи утечки настолько малы, что ими обычно пренебрегают и тогда на схеме замещения (рис. 4.2) конденсатор представляется в виде идеального ёмкостного элемента с ёмкостью C (при учёте токов утечки схема замещения изображается в виде параллельно соединённых идеальных резистивного и ёмкостного элементов).

В результате, полное сопротивление конденсатора Z_конд. принимается равным его ёмкостному сопротивлению X_C:

,

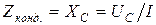где: U_С и I – действующие значения напряжения и тока конденсатора. Ёмкостное сопротивление связано с ёмкостью C следующим образом:

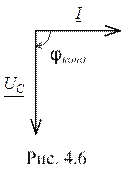Векторная диаграмма тока и напряжения на конденсаторе приведена на рисунке 4.6. Вектор 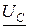напряжения на конденсаторе отстаёт от вектора тока на 90°. Поскольку вектор тока в последовательной цепи, как правило, при построении векторной диаграммы на комплексной плоскости, откладывают по действительной оси, то
вектор 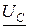будет откладываться в отрицательном направлении мнимой оси (так как он отстаёт от вектора тока на угол
φ_к= –90°<0). В связи с этим ёмкостное сопротивление, обуславливающее ёмкостное напряжение, в комплексном виде записывают как .

В связи с тем, что полное сопротивление конденсатора принимается без активной составляющей, работа на нём не совершается, т. е. активная мощность Р конденсатора равна нулю. Однако в цепи с ёмкостным элементом происходит периодический обмен энергией между источником и электрическим полем данного элемента. Интенсивность такого обмена характеризуют реактивной мощностью:

.

Полная мощность конденсатора равна его реактивной мощности.

Объектами исследования являются индуктивная катушка с постоянными параметрами R, L и батарея конденсаторов, ёмкость которой C можно изменять с помощью переключателей П2 (ёмкость батареи равна сумме емкостей параллельно включенных в неё конденсаторов). Все элементы исследуемой цепи смонтированы на плате № 10 передней панели стенда.

В качестве электроизмерительных приборов при исследовании применяются многопредельный миллиамперметр типа Э-377 и цифровой или стрелочный электронный вольтметр. В качестве источников питания используются: а) однофазный двухполупериодный выпрямитель со сглаживающим фильтром – источник постоянного тока, б) одна из фаз трёхфазного источника – источник переменного тока.

Исследование линейной неразветвлённой
электрической цепи синусоидального тока

Резонансом называется такой режим работы цепи, включающей в себя индуктивные и ёмкостные элементы, при котором её входное сопротивление (входная проводимость) вещественно (т. е. имеет только активную составляющую). Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.

В электрических цепях различают два вида резонанса: резонанс напряжений (при последовательном соединении L и C элементов) и резонанс токов (при параллельном соединении L и C элементов).

В настоящей лабораторной работе исследуется неразветвлённая электрическая цепь, состоящая из последовательно соединённых катушки индуктивности и конденсатора, подключенная к источнику синусоидального тока. Схема цепи представлена на рисунке 5.1.

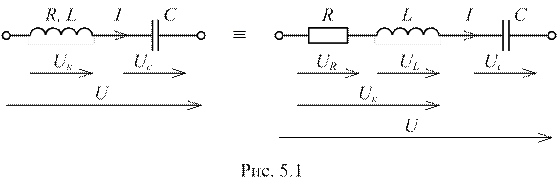
Реальная катушка индуктивности обладает кроме индуктивного сопротивления Х_L ещё и активным сопротивлением R (активное сопротивление проводника, из которого выполняются витки катушки), которое существенно влияет на протекающие в цепи процессы. Поэтому целесообразно реальную цепь представить в виде схемы замещения (рис. 5.1), где катушка индуктивности рассматривается как последовательное соединение идеального резистивного элемента с активным сопротивлением R и идеального индуктивного элемента с индуктивностью L.

В реальном конденсаторе, как и в катушке, наблюдаются потери активной энергии, однако они настолько малы, что ими обычно пренебрегают, поэтому конденсатор на схемах представляется в виде идеального ёмкостного элемента с ёмкостью C (рис. 5.1).

Полное сопротивление цепи, представленной на рисунке 5.1, можно найти по закону Ома:

,

где: U и I – действующие значения напряжения и тока цепи.

Общее сопротивление цепи, состоящей из последовательного соединения R, L и C элементов, должно являться суммой сопротивлений этих элементов. Однако, поскольку сопротивления R, L и C элементов определяются различными факторами (соответственно электрическим сопротивлением металла и сопротивлениями движению тока, обусловленными магнитным и электрическим полями), введено понятие комплексного сопротивления , представляющего общее сопротивление R, L и C элементов в виде комплексного числа. При этом активное сопротивление R рассматривается в качестве вещественной части данного комплексного сопротивления, а реактивное сопротивление X, определяемое разницей индуктивного X_L и ёмкостного X_C сопротивлений (X=X_L–X_C), – в качестве мнимой части:

.

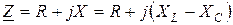Это позволяет активное и реактивное сопротивления рассматривать как две качественно разные части одного целого: R и X откладываются по различным осям на комплексной плоскости, благодаря чему они складываются не как скаляры, а как вектора. Величины реактивных сопротивлений X_L и X_C откладываются по мнимой оси в противоположных направлениях. Вектор тока при построении векторной диаграммы на комплексной плоскости для последовательной цепи, как правило, откладывается по действительной оси, а вектора напряжений на индуктивном и ёмкостном элементах при их углах к току φ_L= +90° и φ_C= –90° соответственно – в положительном и отрицательном направлениях мнимой оси соответственно. По этой причине и реактивные сопротивления X_L и X_C, обуславливающие указанные напряжения, откладываются в положительном и отрицательном направлениях мнимой оси соответственно.

В связи с вышесказанным, полное сопротивление рассматриваемой цепи (рис. 5.1), связано с параметрами своих элементов (R, L, C) следующим образом:

,

где: R, 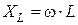, 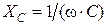– активное, индуктивное и ёмкостное сопротивления соответственно, ω=2∙π·f – угловая частота тока, f – частота тока в цепи. Соотношения активного, реактивного и полного сопротивлений характеризуются треугольником сопротивлений (рис. 5.2), откуда вытекают следующие зависимости:

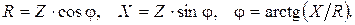
Полное напряжение цепи, изображённой на рисунке 5.1, определяется (аналогично полному сопротивлению) векторной суммой напряжений последовательно соединённых элементов (по второму закону Кирхгофа):

.

Величины , , 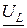и связаны между собой, как стороны треугольника напряжений (рис. 5.3), подобного треугольнику сопротивлений. Треугольник напряжений получается из треугольника сопротивлений, домножением сторон последнего на ток I. Вектор напряжения на резистивном элементе (активная составляющая ) совпадает по направлению с вектором тока , вектор напряжения на индуктивном элементе 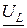(индуктивная составляющая ) опережает вектор тока на 90°, а вектор напряжения на ёмкостном элементе (ёмкостная составляющая ) отстаёт от вектора тока на 90°. Из векторной диаграммы напряжений и тока (рис. 5.3) следует:

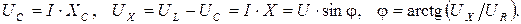
Домножив стороны треугольника сопротивлений на квадрат тока или стороны треугольника напряжений на ток, получим треугольник мощностей (рис. 5.4).

Полная S, активная P и реактивная Q мощности связаны соотношениями:

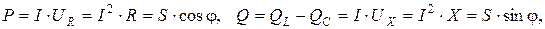
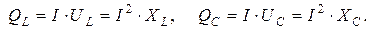
В электрической цепи (рис. 5.1) возможны три различных соотношения параметров Х_L и Х_C:

а) Х_L>Х_C, тогда U_L>U_C, вектор опережает вектор на угол φ, цепь носит индуктивный характер (рис. 5.5–а);

б) Х_L<Х_C, тогда U_L<U_C, вектор отстаёт от вектора на угол φ, цепь носит ёмкостный характер (рис. 5.5–б);

в) Х_L=Х_C, тогда U_L=U_C, вектор совпадает по направлению с вектором (φ=0), цепь работает в режиме резонанса и носит активный характер (рис. 5.5–в).

Режим работы последовательной цепи синусоидального тока, при котором ток и общее напряжение цепи совпадают по фазе, что соответствует совпадению по направлению векторов и на векторной диаграмме, называется резонансом напряжений.

Так как в режиме резонанса реактивное сопротивление всей цепи равно нулю (X=X_L–X_C=0), то и реактивные составляющие всех величин на входе цепи (напряжения, мощности) тоже равны нулю.

Условием резонанса является равенство индуктивного и ёмкостного сопротивлений

или ,

откуда следует, что резонанс наступает при частоте

.

Таким образом, резонанс в цепи может быть получен за счёт изменения одного из следующих параметров: индуктивности катушки L, ёмкости конденсатора C или частоты питающего напряжения f (ω=2∙π·f). В данной работе резонанс напряжений достигается с помощью изменения ёмкости конденсатора.

Так как режим резонанса наступает при X=0, полное сопротивление цепи с последовательным соединением L и C элементов в этот момент достигает наименьшего значения Z_рез.=R, что приводит к существенному возрастанию тока, который достигает максимального значения I_рез:

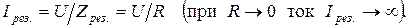
При резонансе напряжений одновременно с ростом тока в цепи увеличиваются и напряжения на индуктивном и ёмкостном элементах (U_L=I∙X_L, U_C=I∙X_C), которые могут во много раз превысить величину напряжения источника питания. Напряжения U_L и U_C имеют одинаковые действующие значения и противоположны по фазе, т. е. на векторной диаграмме векторы 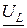и имеют равную длину и направлены в противоположные стороны.

В режиме резонанса коэффициент мощности цепи cos(φ)=P/S, показывающий какую часть от полной мощности составляет активная, достигает максимального значения. Это происходит по причине того, что реактивные мощности на индуктивном и ёмкостном элементах равны (Q_L=Q_C), из чего следует равенство нулю реактивной мощности цепи (Q=Q_L–Q_C=0) и равенство полной и активной мощностей S_рез.=P.

Физическая сущность резонанса заключается в периодическом обмене энергией (реактивной) между магнитным полем индуктивной катушки и электрическим полем конденсатора, причём сумма энергий полей остается постоянной (источник питания цепи в этом обмене реактивной энергией не участвует).

Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако если резонанс возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков.