Энергия заряженных проводников и конденсаторов. Энергия электрического поля

Энергия заряженного проводника распределена в пространстве вне проводника, т.к. внутри проводника напряженность электрического поля E = 0.

Возьмем проводник произвольной формы с зарядом q.

Для того чтобы увеличить его заряд на бесконечно малую величину 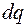, необходимо совершить элементарную работу против сил электростатического поля:

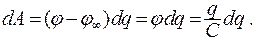(15.25)

Найдем энергию, которой будет обладать проводник

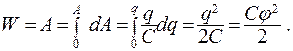(15.26)

Энергия конденсатора сосредоточена между его обкладками. Процесс зарядки конденсатора можно представить как перенос заряда dq с одной его пластины на другую. Пусть потенциал одной пластины j₁ = 0 а другой j₂ = j Элементарная работа внешних сил, совершаемая при переносе зарядов с одной пластины на другую:

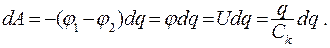(15.27)

Энергия заряженного конденсатора:

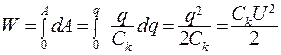(15.28)

Плотностью энергии называется энергия, заключенная в единице объема конденсатора

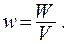(15.29)

Подставим в (15.29) выражение (15.28) и учтем, что емкость плоского конденсатора 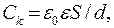а напряжение U связано с напряженностью электрического поля соотношением U = E d .

Плотность энергии w пропорциональна квадрату напряженности электрического поля:

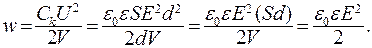(15.30)

В формуле (15.30) объем плоского конденсатора выражен через площадь его пластин и расстояние между пластинами: V = S d. Плотность энергии имеет размерность: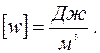

Если известна потенциальная энергия поля, то можно найти силу, действующую между пластинами конденсатора:

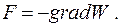
Проекция силы на ось х, вдоль которой направлено электрическое поле в конденсаторе:

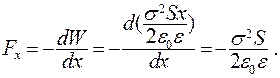(15.31)