Магнитное поле цилиндрического проводника с током

Пусть по бесконечно длинному цилиндрическому проводу радиуса R про­текает по­стоянный ток I . Выберем систему координат x, y, z так, чтобы ось про­вода совпадала с осью координат z (рис. 276).

Будем считать, что ток равномерно распределяется по сечению провода, тогда его плотность будет равна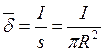

Для исследования магнитного поля выделим две неравнозначные об­ласти, для каж­дой из которых выполним расчет параметров магнитного поля:

1) область внутри провода при 0 £ r £ R ,

2) область вне провода при R £ r £ ¥ .

Для расчета поля во внутренней области выберем контур интегрирования в виде ок­ружности с текущим радиусом r<R . Тогда ток внутри контура интег­рирования:

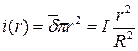, откуда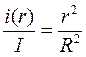

Применим к контуру интегрирования закон полного тока в интеграль­ной форме :

,

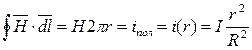откуда следует 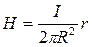и .

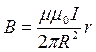Векторы 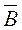и 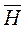направлены по касательной к окружности, их направле­ние опре­деляется по правилу правоходового винта.

При увеличении радиуса на элементарную величину dr произойдет приращение магнитного потока на величину dф на единицу длины провода (l = 1) и приращение магнитного потокосцепления на величину dy :

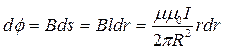
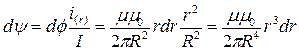
Внутренний магнитный поток и внутреннее потокосцепление найдутся в резуль­тате интегрирования полученных выше выражений по всему сечению провода:

_,

.

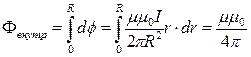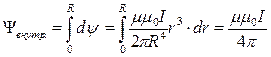Из последнего уравнения следует формула для внутренней индуктив­ности провода на еди­ницу длины :

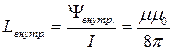[Гн/м]

Внутренняя индуктивность провода зависит от его магнитной прони­цаемости m (для стальных проводов она значительно больше, чем для медных или алюминиевых) и не зави­сит от его радиуса.

Для расчета поля во внешней области выберем контур интегрирования в виде окруж­ности с текущим радиусом r>R . Ток внутри контура интегрирова­ния равен I и не зависит от текущего значения радиуса r. Из закона полного тока следует:

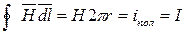, откуда 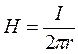и

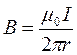
Приращения магнитного потока dф и потокосцепления dy будут равны:

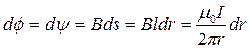
Внешний магнитный поток Ф_внеш и соответственно внешнее потокосце­пление Y_внеш найдутся в результате интегрирования полученных выше выраже­ний по сечению вне про­вода:

,

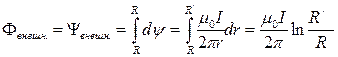где R’ < ¥ - внешний радиус в окружающем провод пространстве, где произво­дится расчет параметров поля.

Внешняя индуктивность провода на единицу длины :

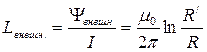[Гн/м]

5. Магнитное поле двухпроводной линии

По двухпроводной линии с заданными геометрическими размерами (рис. 277) (R – радиус проводов, d - расстояние между осями проводов) протекает по­стоянный ток I.

Результирующий вектор магнитной индукции 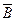в произвольной точке n можно определить по методу наложения как геометрическую сумму состав­ляющих этого вектора 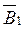и 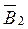от каждого провода в отдельности: 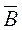= 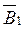+ 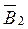. Составляющие вектора 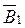и 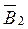определяются по полученным ранее формулам, а их направления – по правилу правоходового винта:

,

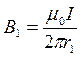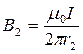
Результирующую индуктивность линии на единицу длины можно найти как сумму индуктивностей прямого и обратного провода:

L = L₁ + L₂ = 2L_внут + 2L _внеш = .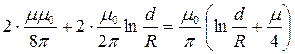

При определении внешней индуктивности провода, внешний радиус ин­тегрирования R следует принять равным расстоянию между проводами d.

Если провода линии выполнены из неферромагнитного материала (Сu, Al) то m=1 и формула для индуктивности линии получит вид:

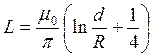[ Гн / м ]

В схемах замещения трехфазных линий электропередачи учитывается ин­дуктивность одного провода (фазы), следовательно:

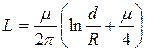[ Гн / м ] – индуктивность каждого провода (фазы) трех­фаз­ной транспонированной ЛЭП на единицу длины, где 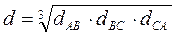– среднегеометрическое значение межосевых расстояний проводов.