Распределение Гиббса

Каноническое распределение Гиббса, связывающее вероятность состояния и энергию:

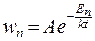(10.5)

где .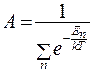

Здесь 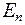- полная энергия, равная сумме кинетической 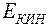и потенциальной 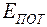энергии всех молекул, образующих систему:

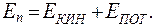
Энергия зависит от координат q и импульсов p молекул: 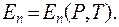В дифференциальной форме распределение Гиббса имеет вид:

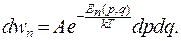(10.6)

Распределение молекул по скоростям Максвелла

Если внешнее поле отсутствует, то полная энергия 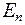в распределении Гиббса равна кинетической энергии 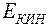, которая может быть записана в виде:

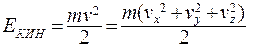(10.7)

В частном случае 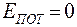из распределения Гиббса следует распределение молекул по скоростям, полученное Максвеллом:

,

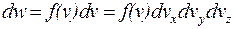где 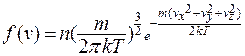- функция распределения молекул по скоростям;

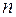- число частиц в единице объёма;

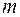- масса частиц;

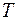- абсолютная температура;

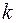- постоянная Больцмана.

Рассмотрим пространство, где вместо координат по осям отложены скорости молекул 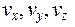(рис.10.2). Точка в этом пространстве соответствует определённой скорости молекулы.

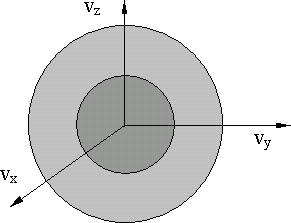
Рис. 10.2.

Распределение точек относительно начала координат в среднем можно считать симметричным, следовательно, плотность частиц в пространстве скоростей r зависит только от модуля скорости :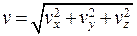

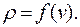
Найдём количество частиц, находящихся в объёме 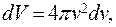заключённом между двумя сферами с радиусами n и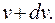

Распределение

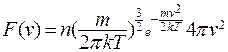(10.8)

называется распределением Максвелла по абсолютным значениям скоростей (рис. 10.3).

Максимальное значение функции распределения 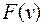соответствует наиболее вероятной скорости молекул:

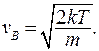(10.9)

Распределение Максвелла позволяет найти среднюю арифметическую скорость:

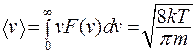(10.10)

и среднюю квадратичную скорость:

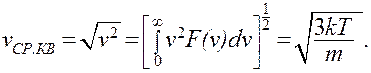(10.11)

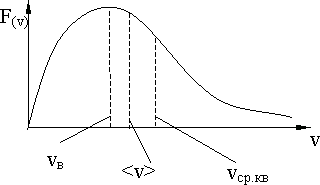
Рис. 10.3.

В опытах О. Штерна распределение Максвелла подтверждено экспериментально. С поверхности нити, покрытой серебром и помещённой вдоль оси вращающегося цилиндра, при нагревании испарялись молекулы. В зависимости от скорости, молекулы попадали в различные точки внутренней поверхности цилиндра.