ГЛАВА 10. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ

Статистический вес

Рассмотрим систему, состоящую из большого количества молекул. Назовем ее макроскопической системой. Состояние такой системы можно описать двумя способами:

1. С помощью средних характеристик системы, например, давления P, объёма V, температуры T, энергии Е. Состояние, заданное характеристиками, усреднёнными по большому числу молекул, будем называть макросостоянием.

2. Путем описания состояния всех образующих тело молекул, для этого необходимо знать координаты q и импульсы p всех молекул. Состояние, заданное таким образом, назовём микросостоянием.

Пусть макроскопическая система является частью какой – либо большой замкнутой системы, будем называть ее средой. Найдём микроскопическое распределение Гиббса, т.е. функцию распределения вероятностей различных состояний макроскопической системы, не взаимодействующей с окружающими телами и имеющей постоянную энергию. Различные состояния системы, имеющие одну и ту же энергию, имеют одинаковую вероятность.

Каждому значению энергии макроскопической системы могут соответствовать различные микросостояния, число таких состояний называется статистическим весом.

Пусть задано макросостояние системы из 4 молекул с помощью параметров: P, V, T, E. Молекулы находятся в сосуде, разделенном проницаемой перегородкой (рис. 10.1а). Cосуд находится в некоторой среде, но не взаимодействует с ней.

Рис. 10.1а. Рис. 10.1б. Рис. 10.1в.

Если все 4 молекулы находятся в правой половине сосуда, то макросостояние системы (0 - 4) можно записать с помощью одного микросостояния, перечислив номера молекул. В этом случае статистический вес .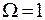

Пусть теперь одна из молекул перешла в левую половину сосуда (рис. 10.1б). Это может быть молекула 1, тогда в правой половине останутся молекулы 2, 3, 4 или это молекула 2, тогда справа останутся молекулы 1, 3, 4 и т.д. Всего возможны 4 различных микросостояния, следовательно, статистический вес макросостояния (1 - 3) .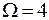

Вероятности всех микросостояний одинаковы. Состояние, когда молекула 1 слева, а 2, 3, 4 справа, имеет такую же вероятность, как состояние, когда молекула 2 слева, а 1, 3, 4 справа. Этот вывод основан на предположении, что все молекулы неотличимы друг от друга.

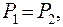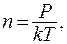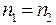Равномерное распределение молекул по обеим половинам сосуда становится очевидным при большом количестве молекул. Мы знаем, что давление выравнивается со временем в обеих половинах сосуда: а поскольку концентрация молекул то и при постоянной температуре одинаковым будет число молекул слева и справа:

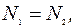
где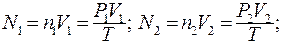

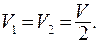
Поскольку наибольшему статистическому весу 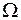соответствует наибольшая вероятность состояния w, то очевидно, вероятность пропорциональна числу состояний. Состояние (2 - 2) является наиболее вероятным, т.к. имеет наибольший статистический вес 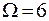(рис. 10.1в).

Энтропия

Для характеристики вероятности состояния вводят энтропию:

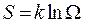(10.1)

где k - постоянная Больцмана.

Пусть 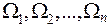статистические веса различных подсистем среды, тогда система будет иметь число микросостояний: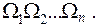

Отсюда находим энтропию замкнутой системы:

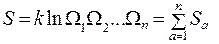
Энтропия сложной системы равна сумме энтропий её частей. В нашем примере мы рассматривали только одну подсистему, статистический вес которой 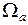зависит от энергии подсистемы 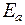. Энтропия также является функцией от энергии:

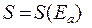
Величина, обратная производной энтропии системы S по её энергии называется абсолютной температурой:

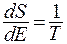(10.2)

отсюда следует

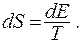(10.3)

Равновесным называется состояние, имеющее наибольший статистический вес. Равновесное состояние не изменяется со временем.

В рассмотренном примере последовательно изучаются равновесные состояния (статистический вес изменяется от 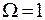до 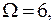образующие стадии равновесного процесса перехода системы в наиболее вероятное из макросостояний. Этот процесс является необратимым, т.к. процесс, обратный ему, является маловероятным. Так, если из одной комнаты газ проник в другую, то невозможно представить, чтобы он через какое - то время опять вернулся в первую комнату.

Вероятность состояния 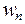системы, находящейся в тепловом контакте со средой, имеющей постоянную температуру T, связана со статистическим весом 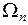соотношением:

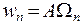
где постоянная нормировки A определяется из условия: 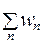(вероятность, что система будет находиться в одном из возможных состояний равна 1).

Статистический вес связан с энтропией данного состояния:

,

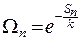а энтропия при Т = const описывается соотношением:

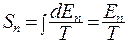. (10.4)