На примере муфт фланцевых

Звенья, соединяющие ведущую и ведомую полумуфты. Первичные операции силового анализа соединительных звеньев многих муфт также во многом однотипны. Заметим, что первоначально силовой анализ проводится для установившегося движения и в его основе лежат условия равновесия в статике. Муфта в целом находится в равновесии относительно оси вращения под действием момента движущего T_рд, приложенного к ведущей полумуфте и момента сопротивления движению T_рс на ведомой полумуфте. Условие равновесия муфты ( 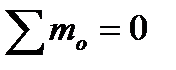) имеет вид T_рд-Т_рс=0, откуда вытекает T_рд=Т_рс=Т_р. Каждая из полумуфт также находиться в равновесии. Равновесное состояние ведущей полумуфты поддерживается моментом T_рд и суммарным моментом сил F_t1c ( 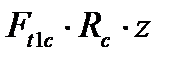) на Z болтах, участвующих в передаче нагрузки. Сила F_t1c приложена к болту со стороны ведомой полумуфты в месте их контакта. Равновесие ведомой полумуфты обеспечивается суммарным моментом движущей силы F_t1д ( 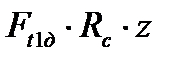) и момента сопротивления Т_рс. Уравнение равновесия полумуфт

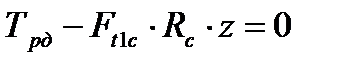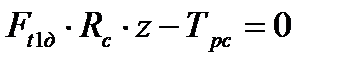; . (4.4)

Равенство T_{рд и} T_рс обусловливает равенство сил F_{t1д и} F_t1c.

С учетом погрешностей изготовления деталей полумуфт (отклонения в радиусе расположения силовых элементов 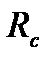, угловом шаге болтов и т.п.) силы 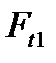не являются равными, что можно учесть коэффициентом неравномерности 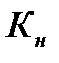. Тогда решение (4.4) относительно 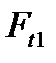принимает вид

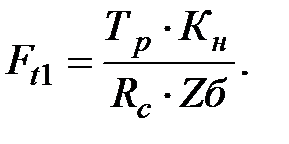(4.5)

Коэффициент 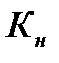в случае отсутствия иных значений можно принимать равным 1,1…1,3. При назначении Z_б в стандартной муфте фланцевой подставляют не общее их число, а только число болтов, поставленных без зазора, которые обычно устанавливаются через один с болтами с зазором. Последние в расчетах принято не учитывать, так же как и момент трения в стыке полумуфт (затяжка болтов не предусматривается).

Как отмечалось в лабораторном занятии (см. подраздел 1.3.1.1) болты, соединяющие фланцы муфты, могут выполнять как функции крепления полумуфт и их центрирования, так и чисто крепежные задачи. В первом случае они устанавливаются без зазора, а во втором – с зазором. Это обстоятельство существенно сказывается и на силовом анализе болтов и на оценке их работоспособности.

Расчетные модели прочностного анализа болтов, установленных без зазора. В случае установки болтов без зазора их тела (на участке установки с натягом диаметром 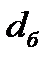) препятствуют повороту полумуфт относительно друг друга под действием момента своим сопротивлением деформациям сдвига и смятия (рис. 4.1 в). Таким образом, в данном расчетном случае к критериям работоспособности болтов следует отнести их прочность на срез

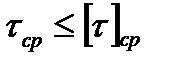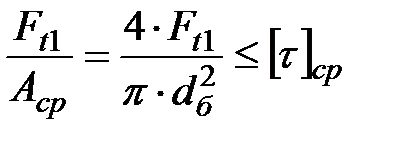или (4.6)

и на смятие

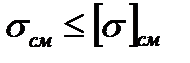или 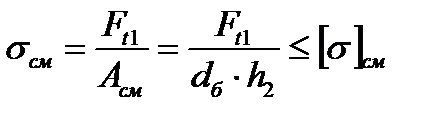, (4.7)

где 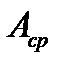, 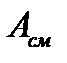– площади среза и смятия соответственно;

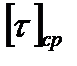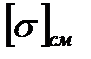, – допускаемые напряжения среза и смятия;

h₂ – минимальная длина участка тела болта, контактирующего с полумуфтой (на рис. 4.1 она увеличена для четкости изображения, а на самом деле она принимается меньше толщины фланца h₁ на 1 – 1,5 мм).

Определение площади площадок среза и смятия одного болта иллюстрирует рис. 4.1 в. Очевидно, площадка среза представляет собой круг, а площадка смятия – полуцилиндр. В расчетах полагают равномерное распределение напряжений среза по сечению, что и отражено в зависимости (4.6). Фактическое распределение 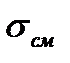в поперечном сечении имеет сложный вид (см. реальную эпюру 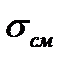на рис.4.1 в). Максимальные и, следовательно, наиболее опасные напряжения 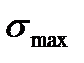имеют место в плоскости действия 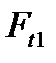в силу наибольшей здесь деформации. Для оценки 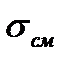прибегают к простому приему – сокращают фактическую площадь смятия (площадь полуцилиндра 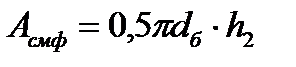) до проекции этой площади на диаметральную плоскость 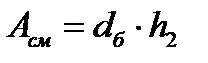. В этом случае средние напряжения весьма близки 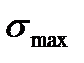на фактической эпюре.

Сформулированные модели для болтов фланцевого соединения, установленных без зазора, могут быть применены при проектировании разнообразных муфт с использованием жестких фланцев, которые предназначаются для передачи крутящего момента. Здесь можно назвать различные модификации зубчатых муфт (см. рис. 1.8), муфты с радиальными пакетами плоских пружин (см. рис. 1.20) и тому подобные в случае, если планируется использование фланцевых соединений с болтами без зазора.

Расчетные модели прочностного анализа болтов, полностью установленных с зазором. Если болты установлены с зазором, то их тело не сопротивляется повороту полумуфт относительно друг друга в пределах зазора между стенкой отверстия и телом болта. Это обстоятельство исключает нормальные условия эксплуатации муфты (дополнительный изгиб болта, относительные повороты полумуфт при реверсе, дополнительные динамические нагрузки и т.п.). Исключение относительного поворота полумуфт в подобных конструкциях достигается за счет организации момента трения Т_fr на поверхности стыка фланцев, отвечающего условию

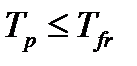.(4.8)

Выражение (4.8) является условием обеспечения работоспособности фланцевого соединения с болтами, установленными с зазором. Для оптимального обеспечения этого условия (Т_р = Т_fr ) на основе расчетной схемы рис. 4.1 г оно может быть записано как

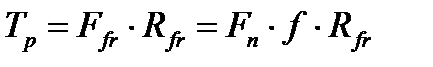, (4.9)

где 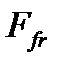– равнодействующая сил трения, распределенных по контактирующим поверхностям фланцев (в дальнейшем для краткости – просто сила трения);

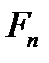– нормальная сила прижатия контактирующих поверхностей, необходимая для создания требующейся силы трения;

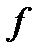– коэффициент трения;

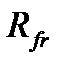– радиус приложения силы трения.

С целью придания выражению (4.9) универсальной формы и возможности его использования для других типов муфт (например, различных фрикционных) введем в это уравнение число поверхностей трения 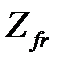, учитывая прямо пропорциональную зависимость момента трения от 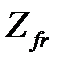. Поверхность трения образуется парой контактирующих поверхностей, стремящихся к сдвигу относительно друг друга. Очевидно, что для фланцевой муфты такая пара является единственной ( 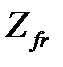=1). При этом (4.9) в универсальном виде запишется как

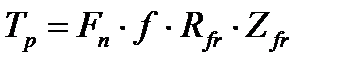. (4.10)

Распределение силы трения по контактирующим поверхностям и, следовательно, радиус, на котором следует приложить 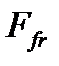, определяются законом распределения по ним удельных давлений q. Распределение последних зависит от способа приложения силы, параллельности трущихся поверхностей, качества их обработки, жесткости дисков и т.д. С позиций обеспечения равномерной нагрузки элементов муфт предпринимают все конструктивные приемы выравнивания q. В рассматриваемой фланцевой муфте это требование достигается количеством болтов и соответствующей жесткостью фланцев (главным образом, их толщиной). В случае равномерного распределения q, следовательно, и сил трения по всей поверхности фланцев, равнодействующая 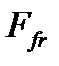смещается к их периферии. С физических позиций она будет расположена на радиусе окружности, делящей поверхность трения на два равновеликих по площади кольца. При построении расчетной модели определения 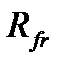можно поступить так. На сопряженнной поверхности фланцев с наружным 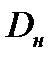и внутренним 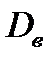диаметрами выделим на радиусе 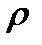кольцо элементарной толщины 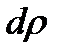. Момент трения на нем при сдавливании постоянным удельным давлением определится по очевидной зависимости

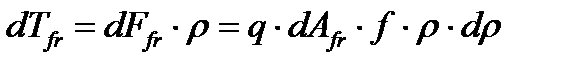, (4.11)

где 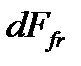– сила трения на выделенном элементарном кольце.

Если учесть, что площадь элементарного кольца 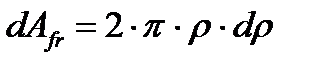, и вновь с целью универсализации расчетной зависимости ввести количество поверхностей трения 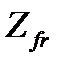, окончательно получим

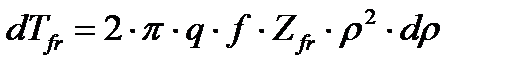. (4.12)

После интегрирования (4.12) получим выражение для оценки полного момента трения на поверхности фланцев

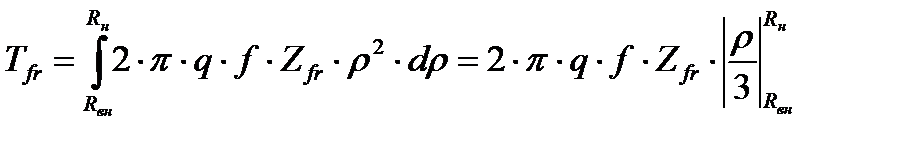. (4.13)

С учетом того, что в качестве нормальной к поверхности трения силы выступает сила затяжки болтов (F_n=F_зат) и удельные давления 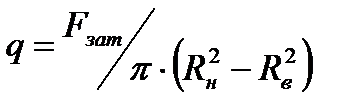, момент трения окончательно определится по зависимости

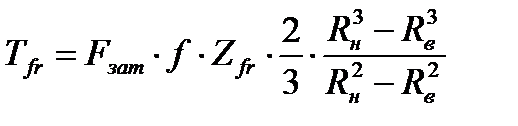. (4.14)

Из сравнения правой части уравнений (4.10) и (4.13) очевидно, что

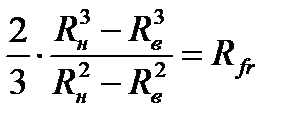. (4.15)

Условие обеспечения работоспособности муфты в целом при установке болтов с зазором (4.8) в оптимальном варианте позволяет вычислить требуемую суммарную силу затяжки установленных 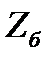болтов:

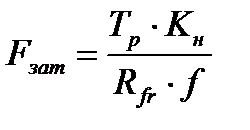. (4.16)

Очевидно, что сила затяжки болтов сжимает фланцы, а сила их упругого сопротивления сжатию будет растягивать болты. Напряжения растяжения в болте, принимая равномерной нагрузку 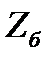, будет

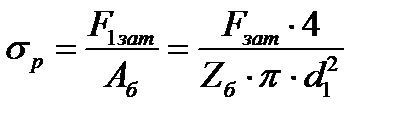, (4.17)

где 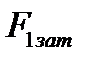– сила затяжки одного болта;

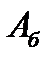– площадь опасного сечения болта, вычисляемая по внутреннему диаметру резьбы .

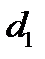Для обеспечения 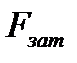при сборке муфты необходимо завернуть резьбовое соединение ключом или гайковертом моментом 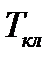. Часть этого момента 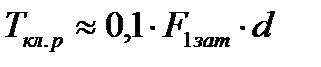, характеризующая сопротивление завинчиванию в резьбе, будет скручивать тело болта (оставшаяся часть момента ключа приложена к торцу гайки и опорной поверхности фланца и в скручивании болта участия не принимает). Напряжения кручения при этом в соответствии (4.1) запишем как

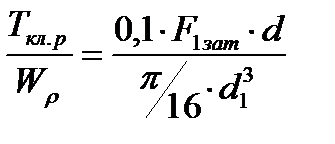. (4.18)

Таким образом, болты во втором варианте имеют сложное нагружение, при котором их прочность оценивается по зквивалентным напряжениям. Для болтов обычно при вычислении используют энергетическую теорию прочности

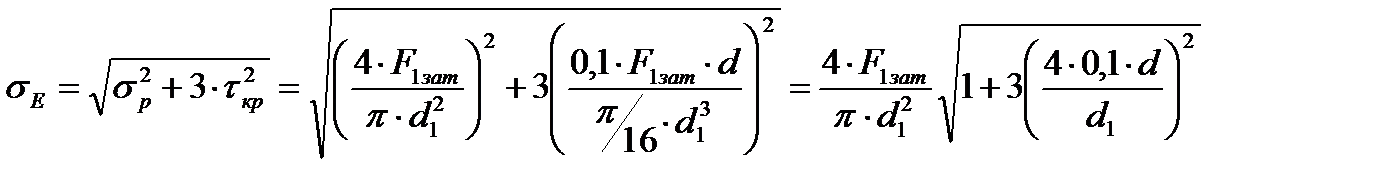. (4.19)

При 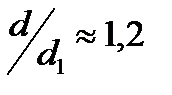в стандартных крепежных резьбах и контролируемой затяжке болтов подкоренное выражение можно принять равным 1,3. Тогда условие прочности болта примет вид

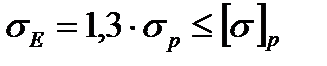. (4.20)

Допускаемые напряжения принимают в соответствии с выбранными материалами болтов и характерными особенностями болтового соединения и его нагружения [4, с. 55 – 60].