Силовой и прочностной анализ оболочковых муфт

на примере муфты с выпуклой оболочкой (см. рис. 1.15)

Неизменным силовым элементом оболочковых муфт, помимо полумуфт, являются разнообразные по конструкции оболочки (выпуклые, вогнутые, составные и т.п.) и болтовые фланцевые соединения. Болтовые соединения предназначены для передачи расчетного крутящего момента с полумуфт на оболочку и наоборот. При этом сила затяжки болтов 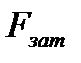обеспечивает создание силы трения 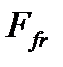на поверхностях контакта упругого элемента с полумуфтой, которая на соответствующем радиусе трения 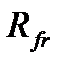образует момент трения 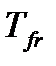(рис. 4.3, разрез Б-Б). Расчетные модели и математические зависимости для определения 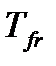, , 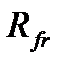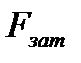рассмотрены на примере фланцевой муфты (см. подраздел 4.1.2). Здесь обратим внимание на расчетное значение количества поверхностей трения 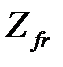. Формально борт оболочки в данной конструкции зажат с двух сторон, однако в расчете принимают 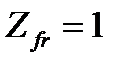, так как зажимные диски не имеют жесткой связи с полумуфтами.

Очевидно, что упругая оболочка подвержена кручению, крутильному сдвигу и сжатию её бортов (рис. 4.3). С позиций кручения можно подвергнуть проверке прочности любые сечения, находящиеся справа и слева вблизи поперечного сечения А-А, в пределах которых толщина оболочки и радиус их расположения от оси вращения практически остаются неизменными. На более удаленных от А-А сечениях толщина оболочки увеличивается за счет перехода к борту, опасность её разрушения снижается. По этой причине прочность оболочки по кручению обычно проверяется по сечению А-А. Математическая модель этого условия (4.1) в оптимуме может быть записана в проверочной форме так:

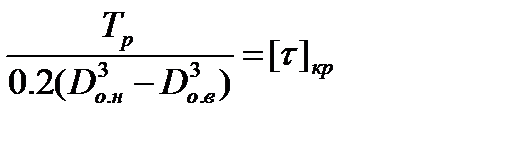. (4.44)

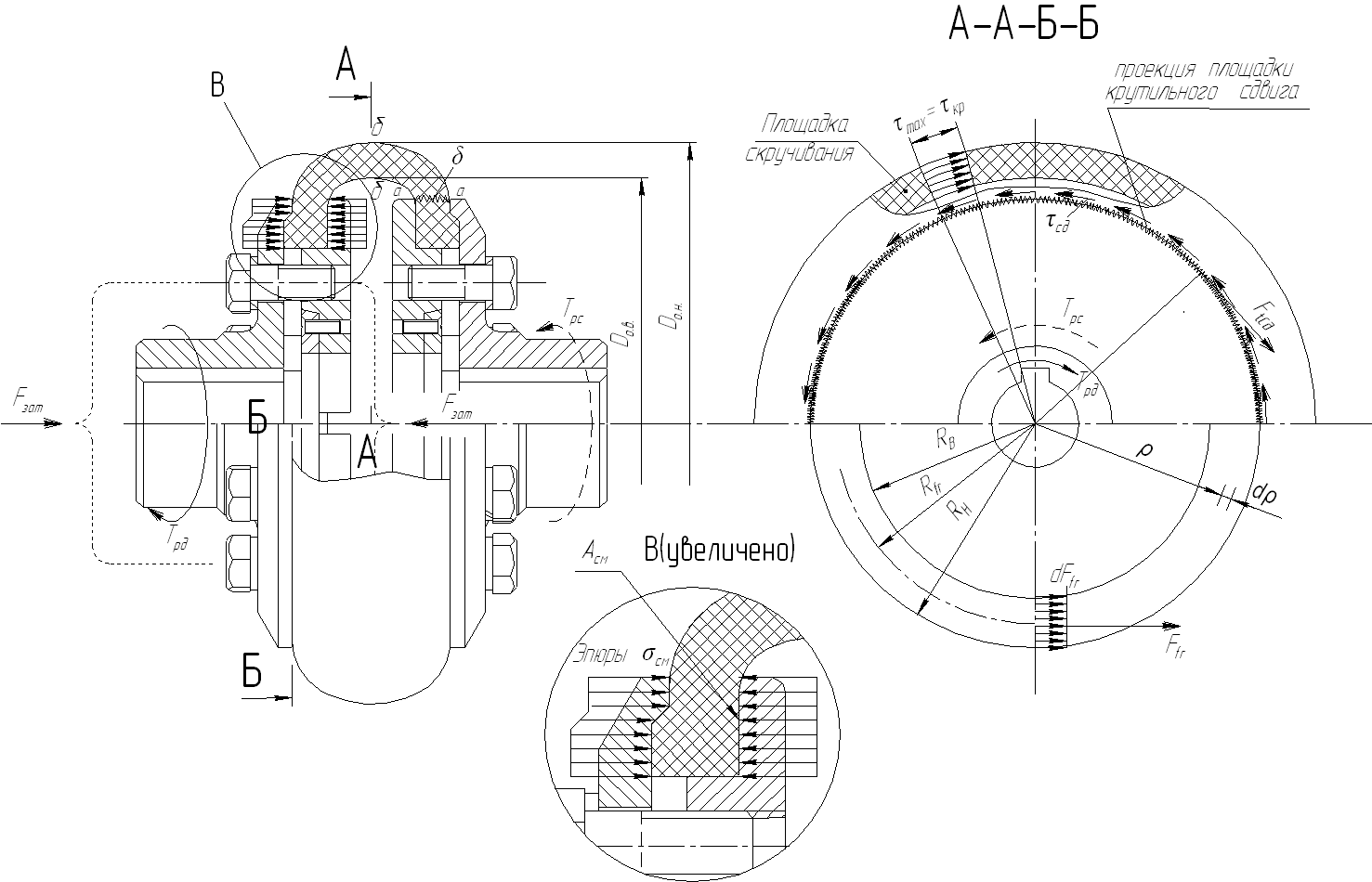
Рис. 4.3. Расчетная модель силового и прочностного анализа муфты оболочковой

При преобразовании в проектную зависимость уравнения (4.44) оно решается относительно одного из неизвестных геометрических параметров, к примеру, наружного диаметра оболочки

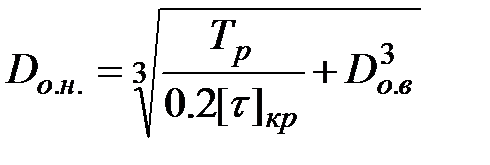. (4.45)

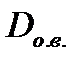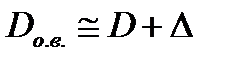Естественно, как во всякой проектной зависимости для её решения придется предварительно задаться имеющими место неизвестными. В данном случае внутренним диаметром оболочки Формулой (4.45) удобно воспользоваться, если, к примеру, в оболочку встраивается дополнительный механизм с заданным внешним диаметральным габаритом D. Тогда с учетом необходимого зазора задают . Если же требуется разместить муфту в ограниченном пространстве, то первоначально целесообразно задаться внешним диаметром оболочки, из уравнения (4.44) установить внутренний диаметр :

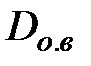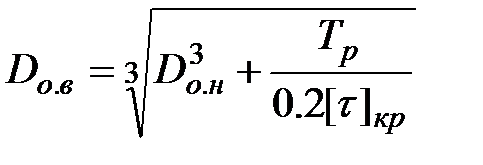. (4.46)

Условие прочности по крутильному сдвигу по площади поверхности цилиндра радиуса R_н, обозначенного на рис. 4.3 волнистой линией:

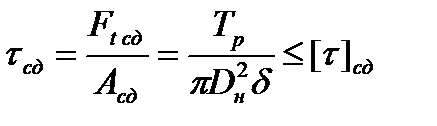. (4.47)

Тангенциальная сила 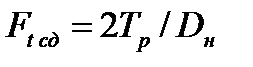, вызывающая сдвиг оболочки по цилиндрической поверхности в месте защемления борта оболочки между фланцами

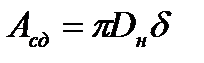( ), показана на рис. 4.3 как движущая сила (по этой причине она направлена в соответствии с движущим моментом 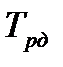). Если при проверке оболочки с размерами, ранее определенными из (4.45 ) или (4.46), условие крутильного сдвига не обеспечивается ( 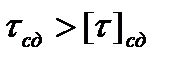), то (4. 47) можно привести к проектной форме с определением требующегося диаметра D_{н. сд}

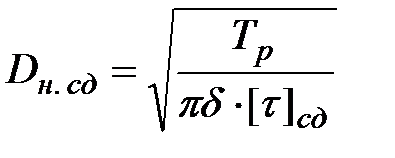. (4.48)

Очевидно, что в подобном случае полученные значения 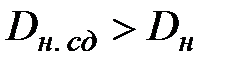, следовательно, в рассматриваемой ситуации более важным критерием работоспособности является не прочность оболочки по кручению, а её прочность по крутильному сдвигу.

Из расчетной схемы (рис. 4.3) видно, что борта оболочки сжимаются силой затяжки 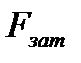. Часто в подобных случаях исключение разрушения детали достигается ограничением напряжений на границе контакта сжимаемых поверхностей 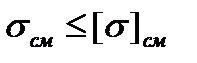. Рабочие напряжения смятия на поверхности кольцевой площадки, обозначенной на расчетной модели, полагают распределенными равномерно (см. эпюры 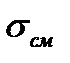). Тогда условие работоспособности по напряжениям смятия примет вид

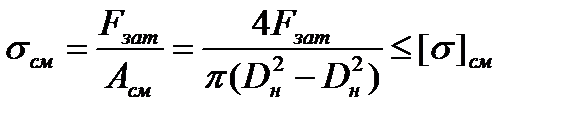. (4.49)