На примере муфты кулачковой

В силовую цепь рассматриваемой муфты входят полумуфта 1, втулка подшипника скольжения 2, опорный стакан пружин 7, регулировочная гайка 9, кулачковая подвижная в осевом направлении втулка 5, неподвижная кулачковая полумуфта 4 и пружины 6 (рис. 4.4) Силовой анализ лучше начать с рассмотрения сил в зацеплении кулачков (рис. 4.5). Формируя расчетную модель этого этапа, примем равномерное распределение удельных давлений (напряжений смятия) по поверхности контакта кулачков при передаче крутящего момента. Обычно без особой погрешности заменяют удельные давления на контактирующих поверхностях равнодействующей F_n, приложенной на среднем диаметре кулачков D_c ≈ (D_н + D_вн) / 2. Более полный подход к определению места приложения равнодействующей изложен в анализе фланцевой муфты. При передаче движущего момента T_рдс ведущего элемента на ведомый равновесие первого поддерживает тангенциальная сила сопротивления F_t1c, а на кулачок ведомого будет действовать движущая сила F_t1д = F_t1c = F_t1 (рис. 4.5 а). Значение F_t1, как отмечено выше, определяется из условия равновесия элементов муфты (4.5). Наклон силы F_t1 к рабочей поверхности кулачка под углом α обусловливает наличие нормальной к ней силы взаимодействия

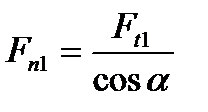(4.50)

и осевой (направленной параллельно оси) составляющей 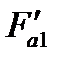. Поскольку при работе муфты наблюдается относительное перемещение кулачков, то необходимо также учитывать силу трения F_fr, которая противодействует выталкиванию кулачков, снижая силу 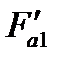. Силу трения на наклонных поверхностях учитывают с помощью угла трения φ, вычитая или прибавляя его к углу наклона в зависимости от направления F_fr. В данном случае

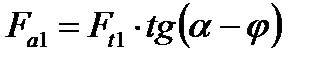. (4.51)

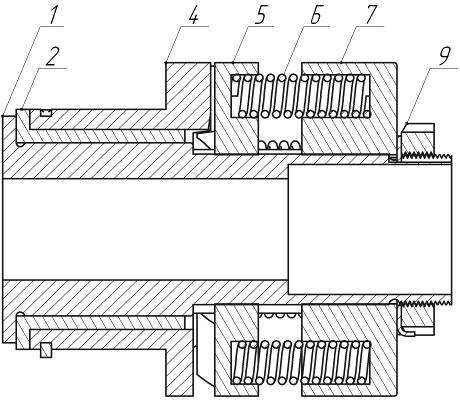
Рис. 4.4. Осевой разрез муфты и ее силовые элементы

Осевые силы, действующие на отдельные кулачки при суммировании, характеризуют требуемую осевую силу нажимного механизма. Однако при определении расчетного значения осевой силы необходимо учесть, что выходу кулачков из зацепления будет препятствовать не только нажимное устройство, но и сила трения подвижной кулачковой втулки о шлицы полумуфты F_frш, которую на основе расчетной схемы (рис. 4.5 б) можно вычислить как

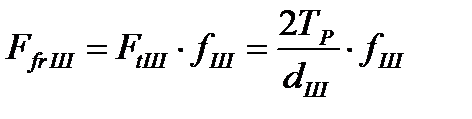, (4.52)

где 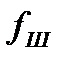– коэффициент трения в шлицах ( 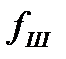≈ 0,15).

Таким образом, окончательное значение суммарной на Z_к кулачках требуемой осевой силы нажимного механизма (пружин в рассматриваемой конструкции):

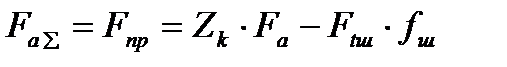. (4.53)

Силовой анализ кулачкового зацепления позволяет ответить на вопрос о нагрузке всех перечисленных выше силовых элементов и прогнозировать их отказы и критерии работоспособности.

Кулачки. Рабочие поверхности кулачков нагружены нормальной силой F_n, реализуемой напряжениями смятия, условие их работоспособности в соответствии с (4.3) запишется так:

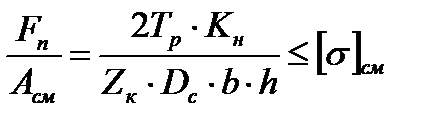, (4.54)

где площадь смятия принята 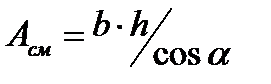. Допускаемые напряжения смятия [σ]_см принимаются из условия предотвращения износа кулачков. С этой же целью материал для кулачковых венцов назначают таким, чтобы при соответствующей химико-термической обработке обеспечивали твердость поверхности не ниже 40 HRc.

Зависимость (4.54) описанными выше методами приводится к проектным формулам решением ее относительно одного из перечисленных параметров Z_k; D_c; b; h. К примеру, относительно среднего диаметра кулачков

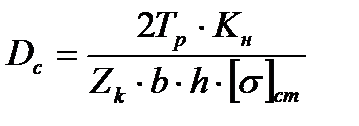. (4.55)

При этом всеми неизвестными параметрами предварительно нужно задаться. Делают эту операцию на основе изучения опыта проектирования кулачковых муфт (общие замечания по этому поводу см. подраздел 4.1.3).

Тело кулачка подвергается изгибу силой 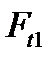. Расчетная модель строится на принятии кулачка условно в виде жестко защемленной балки с нагрузкой, приложенной к вершине кулачка (см. рис. 4.5 в). Уравнение прочности по изгибным напряжениям (4.40) применительно к обсуждаемой муфте примет вид

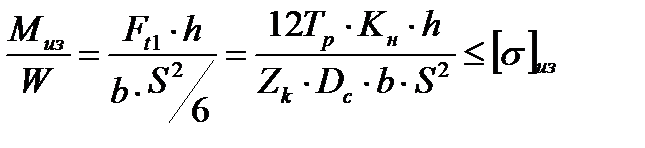. (4.56)

Осевой момент инерции опасного сечения у основания кулачка принят условно как для прямоугольника с размерами b и S, которые обозначены пунктиром на рис. 4.5 в. Проверочная зависимость (4.40) также может быть преобразована в проектную, если изгибное разрушение кулачка становится наиболее опасным отказом. Последнее случается крайне редко, по причине чего расчет на изгиб кулачка обычно не производится.

Полумуфта 1. Тело полумуфты передает крутящий момент Т_р с вала на подвижную кулачковую втулку или наоборот и работает на кручение. Математические модели проверочных и проектных расчетов в подобных случаях рассмотрены выше применительно к фланцевым муфтам (см. подразделы 4.1.2 и 4.1.1). В качестве расчетного сечения следует принять минимальное по размерам ее сечение 1-1 по канавке для выхода фрезы при нарезании шлиц (см. рис. 4.4). Там же изложен и расчет шпоночного паза. Силовым элементом полумуфты также является шлицевое соединение с подвижной кулачковой втулкой. Расчет шлицевых соединений основан на обеспечении прочности по напряжениям смятия и износостойкости рабочих поверхностей.

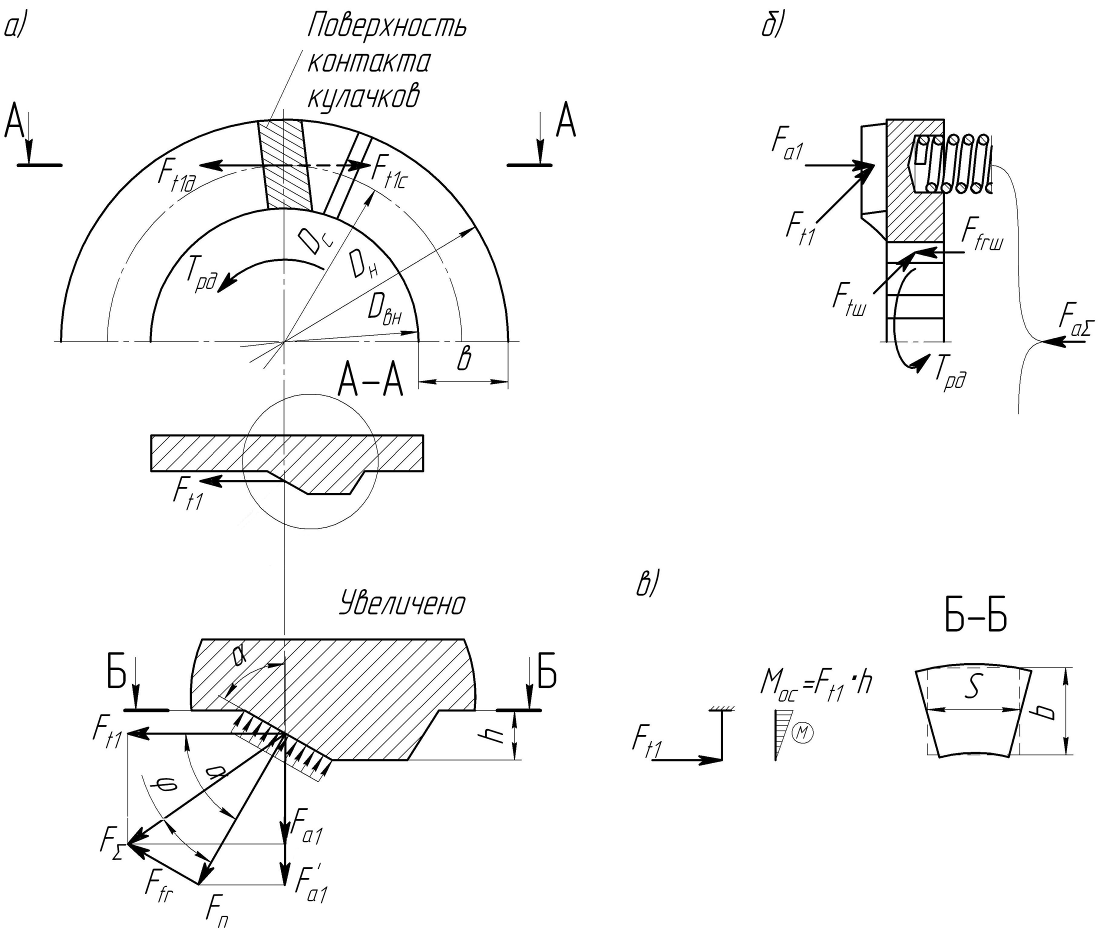
Рис. 4.5. Расчетные модели силового и прочностного анализа

кулачковой предохранительной муфты: а – кулачкового зацепления;

б – требуемой осевой силы пружин (нажимного механизма); в – изгибной прочности кулачков

Применительно к шлицам подвижной втулки более значимым является критерий износостойкости. По принятой универсальной методике расчет для обоих критериев проводится по напряжениям смятия [4]. Математическая модель критерия (4.7) в данном случае приобретает вид

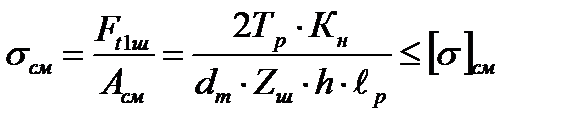, (4.57)

где 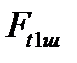– тангенциальная сила, нагружающая один из 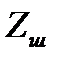шлиц;

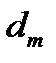– средний диаметр шлицевого соединения;

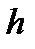– высота шлица;

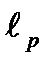– рабочая (совместная) длина шлица.

Допустимые напряжения смятия [σ]_см для подвижных шлицевых соединений, в которых перемещение происходит под нагрузкой, принимают в диапазоне (5…15) МПа. При этом материалы деталей соединения должны обеспечивать твердость рабочих поверхностей не ниже 40 HRc.

Отмеченные геометрические параметры шлиц первоначально назначаются в соответствии с принятым стандартом на них по наружному диаметру участка полумуфты под шлицы. Затем по (4.57) подвергаются проверочному расчету. Если размеры шлиц не обеспечивают соблюдение этого критерия, то есть шлицы являются слабым элементом в звене «полумуфта – подвижная кулачковая втулка», то в распоряжении конструктора можно выделить три переменные проектирования: увеличение длины l_p, диаметра d_m и изменение типа шлиц. В первых двух случаях (4.57) решают соответственно относительно требуемых значений l_p или d_m.

Кроме названных силовых элементов полумуфты, следует также назвать резьбу, нагруженную через гайку силой пружин F_пр. Под действием этой силы тело полумуфты растягивается, а витки резьбы срезаются и сминаются (в силовых резьбах более опасными считаются напряжения среза). По установившейся методике расчетов резьбовых соединений проверяют прочность растягиваемых элементов (в нашем случае прочность тела полумуфты), а работоспособность резьбы обеспечивается автоматически в силу принципа равнопрочности, заложенного в конструкцию стандартных гаек.

Втулка подшипника скольжения. Нагрузка на подшипник определяется степенью равномерности распределения окружных (тангенциальных) сил 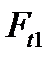между кулачками. При абсолютном равенстве 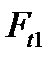на всех кулачках сила, нагружающая вал и подшипники, отсутствует. При реальной точности изготовления деталей муфты равнодействующая приведенных к валу сил не равна нулю. Обычно принимают радиальную нагрузку на валы (подшипники):

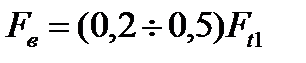. (4.58)

Критерием работоспособности подшипников скольжения наиболее часто является износостойкость, условие которой в простейшем случае обеспечивается ограничением удельных давлений 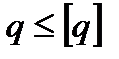. Рассматриваемый подшипник работает лишь при срабатывании муфты. По этой причине он, как правило, не является слабым элементом и его расчет опущен.

Подвижная кулачковая втулка. Силовой и прочностной анализ кулачков проведен выше и в дополнительных комментариях не нуждается. Тело втулки передает расчетный крутящий момент с кулачков на шлицы либо наоборот. Расчет втулки на крутильную прочность аналогичен расчету полумуфт. В качестве проверочных и проектировочных зависимостей, используя метод аналогии, можно применять (4.1), (4.21), (4.22).

Другим силовым элементом кулачковой втулки являются шлицы, которые передают крутящий момент Т_р с полумуфты на рассматриваемую деталь или наоборот. Прочностной анализ шлиц выполнен выше применительно к полумуфте.

Кулачковый венец втулки также подвержен сжатию осевой составляющей силы взаимодействия кулачков 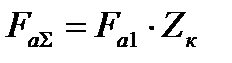и уравновешивающей ее силой пружин 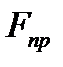. Уровень напряжений сжатия в венце низок и на работоспособность втулки практического влияния не оказывает. По этой причине расчет втулки по напряжениям 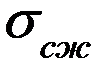не производится.

Опорный стакан пружин. Регулировочная гайка. Эти детали находятся под действием силы F_пр. Напряжения сжатия в опорном стакане, как и в предыдущем случае, невелики и на его работоспособность не влияют. Размеры стакана назначаются из конструктивных соображений: наружный диаметр стакана и размеры шлиц принимают в соответствии с размерами кулачковой втулки, отверстий под пружины – по наружному диаметру пружин. В качестве регулировочной используют гайку круглую шлицевую по ГОСТ 8530 – 90. Как отмечено, при анализе полумуфт прочность резьбы обеспечивается в соответствии с принципом равнопрочности, заложенным при конструировании стандартных резьбовых деталей.

Пружины. Используемые в кулачковой муфте пружины сжатия нагружены силой 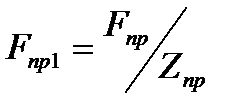, где 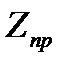– количество установленных пружин. Под действием этой силы каждый из витков нагружается крутящим моментом Т_пр. Наличие этого момента поясняет рис. 4.6. Осевая сила F_пр1 относительно любого из сечений витков создает момент, равный 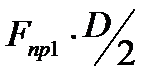, который уравновешивается моментом сопротивления скручиванию витка T_пр. Отсюда

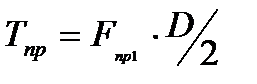. (4.59)

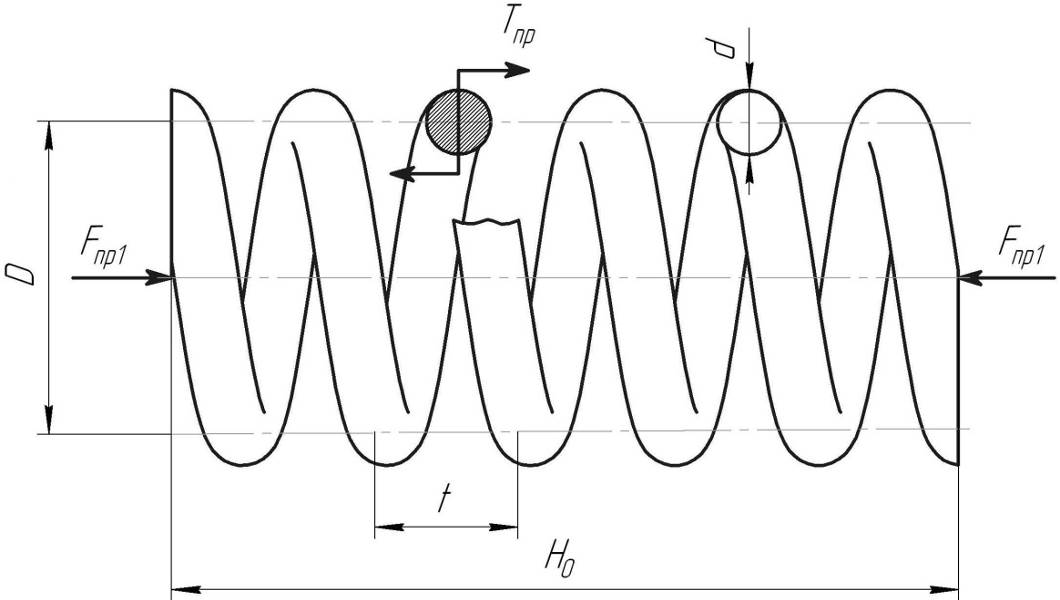
Рис. 4.6. Силовой анализ пружины и ее геометрия

Основным критерием работоспособности пружин считают прочность по напряжениям кручения под действием момента T_пр. Математическая модель этого критерия (4.1) применительно к пружинам с круглым профилем проволоки записывается так:

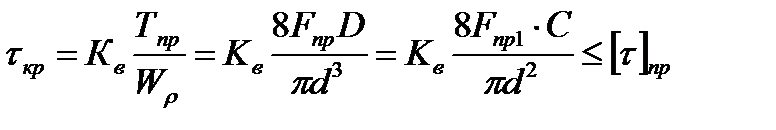. (4.60)

Геометрические параметры пружины D и d (соответственно средний диаметр пружины и диаметр ее проволоки) обозначены на рис. 4.6. Коэффициент К_в, дополнительно введенный в (4.60), учитывает кривизну витков пружины и назначается по таблицам в зависимости от индекса пружины С [5]. Индекс пружины определяется соотношением 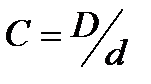. Для оптимального соотношения 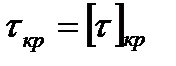(4.1) может быть преобразовано в проектную зависимость. Если решить уравнение относительно диаметра проволоки, то

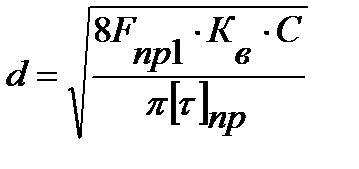. (4.61)

Как всегда при проектных расчетах предварительно необходимо задаться неизвестными: 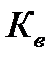и С. Поскольку 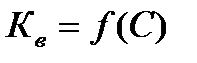, то решение задачи следует начать с назначения индекса пружины. Инженерной практикой выработан диапазон широко используемых значений С = 4…12. Указанный диапазон С зависит от вычисляемого диаметра проволоки. Поэтому решается задача в итерационном режиме. Первоначально задаются значением С в зависимости от ожидаемого диаметра проволоки. Если полученный диаметр d не соответствует ориентировочно принятому, то расчет повторяют с корректировкой С. Для назначения С и 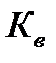можно воспользоваться таблицей.

К назначению индекса пружины и коэффициента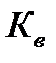

	Ожидаемый диаметр проволоки d
d ≤ 2,5 мм – С = 5…12; d = (3…5)мм – С = 4…10; d = (6…12)мм – С = 4…9.
С
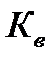
	1,37	1,29	1,24	1,17	1,14	1,11

При назначении индекса пружин следует руководствоваться следующими соображениями. Увеличение С в случае сохранения числа витков пружины приводит к увеличению диаметральных габаритов пружин и увеличению их податливости. Увеличение размера пружин и в конечном итоге муфты, естественно, противоречит задаче получения минимальных размеров и материалоемкости обсуждаемого устройства. Однако при этом улучшаются такие эксплуатационные показатели работы муфты как снижение перегрузки при срабатывании кулачкового механизма, повышение точности срабатывания. Упругие характеристики двух различных по жесткости пружин приведены на рис. 4.7 .

Сравнение упругих характеристик податливой 1 и жесткой 2 пружин показывает, что для получения необходимой силы прижатия кулачков F_пр жесткую пружину необходимо деформировать на меньшую величину 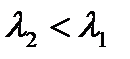. При срабатывании муфты кулачки перемещаются в осевом направлении и дополнительно деформируют пружины на величину ∆λ, равную высоте кулачков h. В силу разной жесткости пружин на равную величину их дополнительной деформации они откликаются разными значениями прироста силы, причем ∆F₁ < ∆F₂ (прирост сил в сравниваемых пружинах). Следовательно, и силы срабатывания F_{1пр max} < F_{2пр max} и крутящие моменты T_1max < T_2max 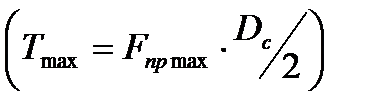(рис. 4.7). Таким образом, использование податливых пружин снижает перегрузку элементов приводов, а также повышает точность срабатывания.

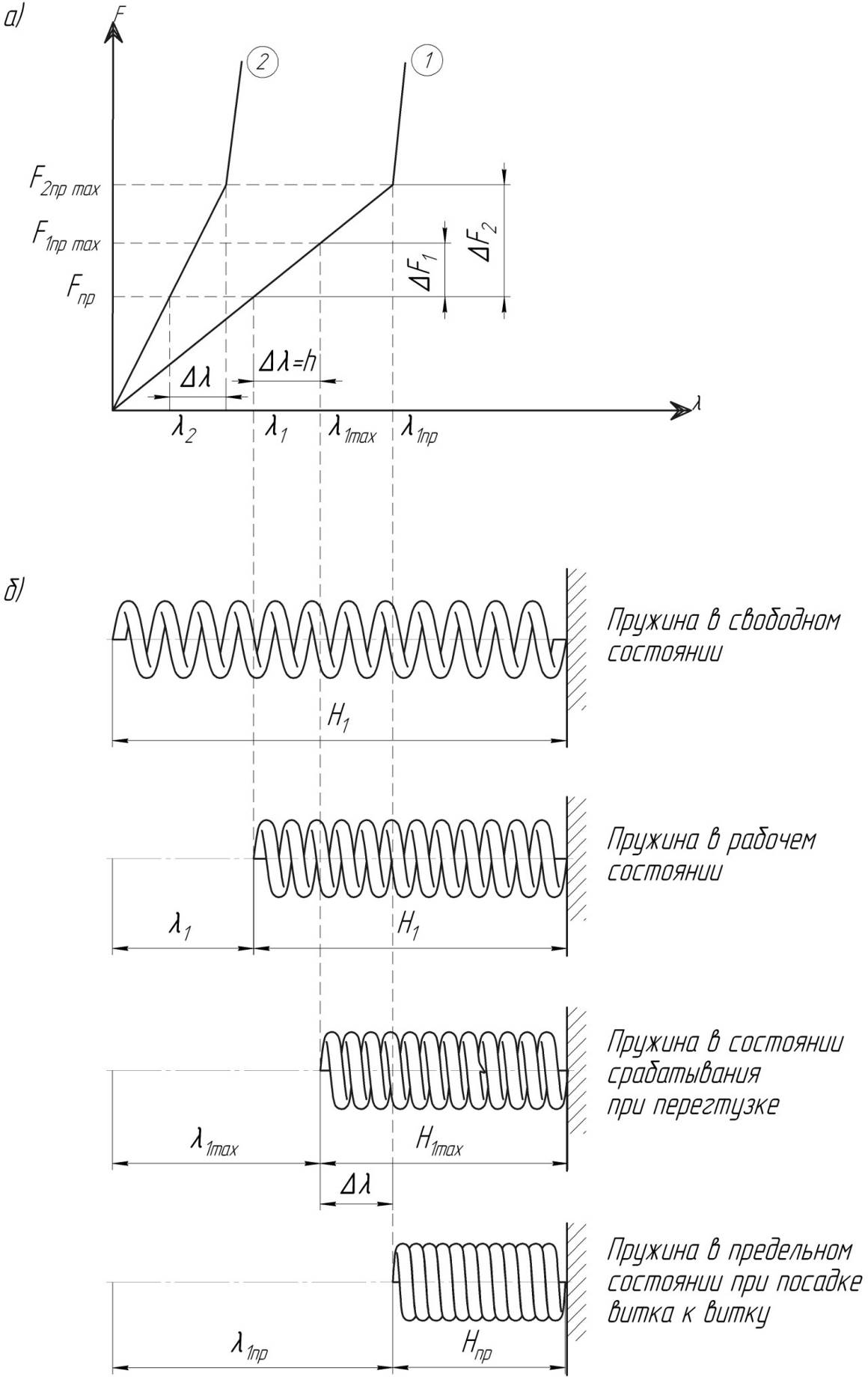
Рис. 4.7. Сравнительные характеристики пружин различной жесткости