Построить биссектрису данного угла.
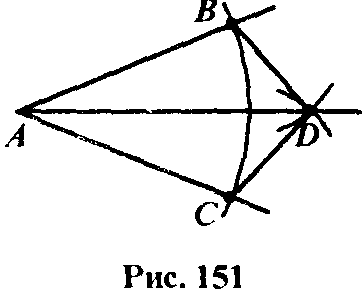
| Рис. 15 |
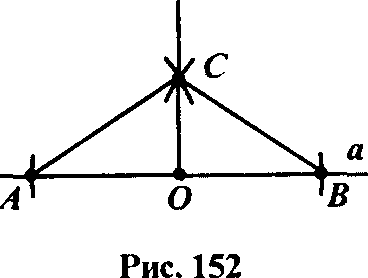
| Рис. 16 |
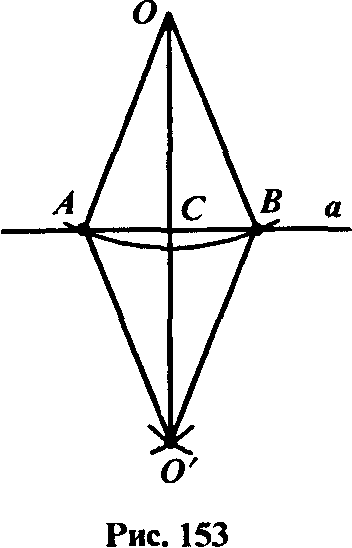
| Рис. 17 |
1) точка О лежит на прямой а;
2) точка О не лежит на прямой а.
В первом случае построение выполняется так же, как и в задаче 4, потому что перпендикуляр из точки О, лежащей на прямой, - это биссектриса развернутого угла (рис. 16).
Во втором случае из точки О как из центра проводим окружность, пересекающую прямую а (рис. 17), а затем из точек А и В тем же радиусом проводим еще две окружности. Пусть О' - точка их пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка О. Прямая 00' и есть перпендикуляр к данной прямой а. Докажем это.
Обозначим через С точку пересечения прямых АВ и ОО'. Треугольники АОВ и АО'В равны по трем сторонам. Поэтому угол ОАС равен углу О'АС и, значит, треугольники ОАС и О'АС равны по двум сторонам и углу между ними. Отсюда их углы АСО и АСО' равны. А так как углы смежные, то они прямые. Таким образом, ОС есть перпендикуляр к прямой а.
Дата добавления: 2021-01-26; просмотров: 682;











