ПРАКТИЧЕСКАЯ РАБОТА. МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

Цель. Рассмотреть общие подходы к изучению понятий в начальном курсе математики, овладеть знаниями об объеме и содержании математических понятий, об отношениях между понятиями и о видах определений понятий, а также правилах конструирования определений, через род и видовое отличие.

Теоретическая часть

Вопросы к изучению

1. Математические понятия.

2. Объем и содержание понятия.

3. Отношения рода и вида между понятиями.

4. Определение понятий.

5. Требования к определению понятий.

6. Неявные определения.

Представления о математических понятиях -

Ø это понятия об идеальных объектах;

Ø каждое математическое понятие имеет название (термин), объем и содержание;

Ø математические понятия могут находиться в отношении рода и вида, если их объемы находятся в отношении включения, но не совпадают;

Ø математические понятия могут быть тождественными, если их объемы совпадают;

Ø понятиям дают определения; они могут быть явными и неявными; к неявным относят контекстуальные и остенсивные определения; среди явных чаще всего используются определения через род и видовое отличие;

Ø при воспроизведении или конструировании определений через род и видовое отличие необходимо соблюдать ряд правил: определение должно быть соразмерным, в нем не должно быть порочного круга, оно должно быть ясным.

Обозначения

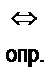- «есть (по определению)»;

а 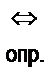в – а есть (по определению) в, где а первое понятие, а в – второе понятие.

а 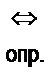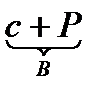- определение через род и видовое отличие, где а - определяемое понятие, в - определяющее понятие, с - родовое понятие (по отношению к определяемому), а видовое отличие – Р.

Практическая часть

Обязательные задания

1. Начертите три геометрические фигуры, принадлежащие объему понятия: а) параллелограмм; б) трапеция; в) окружность.

2. Назовите пять существенных свойств понятия: а) треугольник; б) круг.

3. Каков объем понятия: а) однозначное число; б) натуральное число; в) луч?

4. Назовите несколько свойств, общих для прямоугольника и квадрата. Какое из следующих утверждений верное: а) Всякое свойство квадрата присуще прямоугольнику. б) Всякое свойство прямоугольника присуще квадрату?

5. Находятся ли в отношении рода и вида следующие пары понятий: а) многоугольник и треугольник; б) угол и острый угол; в) луч и прямая; г) ромб и квадрат; д) круг и окружность?

6. Изобразите при помощи кругов Эйлера отношения между объемами понятий а, в и с, если: а) а – «четырехугольник», в – «трапеция», с – «прямоугольник»; б) а – «натуральное число, кратное 3», в – «натуральное число, кратное 4», с – «натуральное число»; в) а – «треугольник», в – «равнобедренный треугольник», с – «равносторонний треугольник».

7.

С

В

А

Приведите примеры понятий, отношения между которыми изображены на рисунке.

а) б)

С

А

В

8. Среди понятий, изучаемых в начальном курсе математики, есть такие, как «четное число», «треугольник», «многоугольник», «число», «трехзначное число», «прямой угол», «сумма», «слагаемое», «выражение». Есть ли среди них понятия, находящиеся в отношении: а) рода и вида; б) целого и части?

9. Какие свойства понятий «прямоугольник» и «сложение» изучают в начальном курсе математики?

10. Переформулируйте следующие определения, используя слова «тогда и только тогда, когда»:

а) Четным называется число, которое делится на 2.

б) Множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В.

в) Множества А и В называются равными, если А Ì В и В Ì А.

г) Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.

11. В следующих определениях выделите определяемое и определяющее понятие, родовое понятие (по отношению к определяемому) и видовое отличие: а) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны; б) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

12. Назовите все свойства, которые содержатся в видовом отличии каждого из следующих определений: а) Биссектрисой угла называется луч, выходящий из вершины угла и делящий угол пополам; б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

13. Соразмеримы ли следующие определения: а) Остроугольным треугольником называется треугольник, у которого есть острый угол; б) Прямоугольным треугольником называется треугольник, у которого есть прямой угол.

14. Учащийся определил прямой угол, стороны которого взаимно перпендикулярны, а взаимно перпендикулярные прямые как прямые, образующие при пересечении прямые углы. Какую ошибку допустил учащийся?

15. Есть ли логические ошибки в следующих определениях? Если есть, то исправьте их.

а) Прямоугольником называется четырехугольник, у которого противоположные стороны равны.

б) Биссектрисой угла называется прямая, делящая угол пополам.

в) Сложением называется действие, при котором числа складываются.

г) Равносторонним треугольником называется треугольник, у которого равны все стороны и все углы.

д) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны.

16. Дайте определение: тупоугольного треугольника, равнобедренного треугольника, трапеции. Какие понятия вы выбрали в качестве родового в каждом случае? Какие свойства включили в видовое отличие?

Творческие задания

1. Что нужно сделать, чтобы проверить непустоту понятий: а) «параллельные прямые», б) «прямоугольник», в) «число 1000000».

2. Объясните, почему следующее определение разности множеств является широким: «разностью множеств А\В называется множество элементов А, не принадлежащих В».

3. Понятие «противоположные стороны прямоугольника» в начальном курсе математики можно определить так: «Красным цветом обозначены две противоположные стороны прямоугольника. А синим цветом – две другие противоположные стороны» (все это показано на рисунке). Какой способ определения понятия использован?

4. Выясните, каким способом определяются в различных учебниках по математике для начальных классов понятия: а) выражение; б) четное число; в) сумма; г) однозначное число; д) слагаемое; е) умножение.