ПРАКТИЧЕСКАЯ РАБОТА. ВЫСКАЗЫВАНИЯ И ВЫСКАЗЫВАТЕЛЬНЫЕ ФОРМЫ

Цель. Рассмотреть общие подходы к изучению математических предложений в начальном курсе математики, уметь раскрыть их логическую структуру. Рассмотреть правила определения значения истинности составного высказывания и нахождение множества истинности составных высказывательных форм.

Теоретическая часть

Вопросы к изучению

1. Высказывания и высказывательные формы.

2. Конъюнкция и дизъюнкция высказываний.

3. Конъюнкция и дизъюнкция высказывательных форм.

Основные понятия темы

Ø высказывание;

Ø значение истинности высказывания;

Ø высказывательная форма;

Ø область определения высказывательной формы;

Ø множество истинности высказывательной формы;

Ø элементарные высказывания;

Ø логические связки;

Ø составные высказывания;

Ø конъюнкция высказываний и высказывательных форм;

Ø дизъюнкция высказываний и высказывательных форм.

Правила

Ø определения значения истинности составного высказывания;

Ø нахождения множества истинности составных высказывательных форм: Т _{А Ù В} = Т_А Ç Т _В, Т _{А Ú В} = Т_А È Т _В,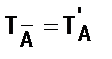

Обозначения

А Ù В – составное высказывание, читают «А и В»;

А Ú В – составное высказывание, читают «А или В»

Практическая часть

Обязательные задания

1. Среди следующих предложений, рассматриваемых в начальном курсе математики, укажите высказывания и определите их значение истинности: а) (12-7)×(6+3)=45; б) (15+12) : 3>10; в) в любом прямоугольнике противоположные стороны равны; г) (12 – х) × 4 =24; д) среди четырехугольников есть такие, у которых все стороны равны; е) число z – двузначное; ж) произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174; з) число 6 является корнем уравнения (12 – х) × 4=24.

2. Какие предложения из упражнения 1 являются высказывательными формами? Подставьте в них значение переменной так, чтобы получилось: а) истинное высказывание; б) ложное высказывание.

3. Можно ли считать высказывательными формами следующие записи: а) х² – 2х; б) 7×4+2=30; в) 4х +2у; г) 7×4 +2 < 30?

4. Найдите множество истинности высказывательной формы 2х – 10<0, заданной на множестве Х, если: а) х > 2; б) 2< х < 6; в) 2< х £ 6; г) х £ 3; д) 2£х<6; е) 2 £ х £ 6. Как можно записать, используя общепринятые символы, множество истинности каждого из данных предложений?

5. Изобразите на координатной плоскости множества истинности следующих предложений при условии, что х, у ÎR: а) х = у; б) х = 2; в) у = 2х + 3; г)у = 2х; д) у = 2; е) у = 2х –3.

6. В следующих составных предложениях выделите составляющие их элементарные предложения и логические связки: а) В равнобедренном треугольнике АВС биссектриса ВD является медианой и высотой; б) х³7; в) Если запись числа оканчивается цифрой 0, то число делится на 5; г) Треугольник является равносторонним тогда и только тогда, когда все его углы равны; д)Неверно, что число 17 делится на 3; е) Если а×в = 0, то а = 0 или в =0.

7. Какова логическая структура (форма) следующих предложений: а)Средняя линия треугольника параллельна основанию и равна его половине; б)Если число делится на 2 и на 3, то оно делится на 6; в) Треугольник АВС не является равносторонним.

8. Приведите примеры математических предложений, имеющих логическую структуру вида: а) А и В; б) А или В; в) если А, то В.

9. Известно, что высказывание А истинно. Можно ли, зная лишь это, определить значение истинности высказывания: а) А Ú В; б) А Ù В?

10. Известно, что высказывание А – ложно. Можно ли, зная лишь это, определить значение истинности высказывания: а) А Ú В; б) А Ù В?

11. Определите значение истинности каждого высказывания: а) число 6 делится на 2 и на 3; б) число 123 делится на 3 и на 9; в) при делении 42 на 5 в остатке получится 2 или 5; г) 3£7; ж) 3³7.

12. Каждое из следующих предложений замените конъюнкцией либо дизъюнкцией, имеющей тот же смысл: а) число 7 принадлежит хотя бы одному из множеств А и В; б) квадратное уравнение имеет не более двух корней; в) каждое слагаемое суммы х+у+z делится на 3; г) по крайней мере одно из натуральных чисел n, n-1, n+1 четно.

13. Покажите, что, выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции высказывательных форм:

а) Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30. Выпишите все числа, в записи которых: 1) три цифры и есть цифра 3; 2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите те числа, которые: 1) делятся на 3 и 9; 2) делятся на 3 или на 9.

14. Выполните следующие задания и дайте обоснование предложенным ответам:

а) Постройте по два треугольника, принадлежащих множеству А, если оно состоит из: 1) прямоугольных и равнобедренных треугольников; 2) прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых: 1) диагонали равны и есть прямой угол; 2) диагонали равны или есть прямой угол.

в) Запишите три числа, которые: 1) делятся на 4 и больше 12; 2) делятся на 4 или 12.

15. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

а) 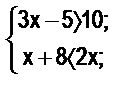б)

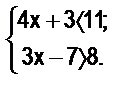
16. Решите уравнение (х-3)×(х+2) ×(х-7)=0, х ÎR. Использовалось ли вами понятие дизъюнкции высказывательных форм?

17. Вместо многоточия вставьте «и» либо «или»: а) х ÎAÇB тогда и только тогда, когда хÎA …х ÎВ. б) хÎAÈB тогда и только тогда, когда хÎA …хÎВ.

18. Пусть А – множество ромбов, В – множество прямоугольников. Как называется четырехугольник, являющийся одновременно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В?

Творческие задания

1. А – множество четных натуральных чисел, В – множество натуральных чисел, меньших 20. Установите, какие из следующих высказываний истинны:

а) 5ÎA или 5ÎB; д) 44 Î А или 44 ÎВ;

б) 5 Î А и 5 Î В; е) 44 Î А и 44 Î В;

в) 8 Î А или 8 Î В; ж) 51 Î А или 51 ÎВ;

г) 8 ÎА и 8 ÎВ; з) 51 Î А и 51 Î В.

2. Покажите, что выполнение учащимися начальных классов следующих заданий связано с понятием высказывательной формы, области ее определения и множества истинности: а) Из ряда чисел 1, 2, 3, 4, 5, 6, 7, 8, 9 выпишите, которые делятся на 3; б) Назови все числа, меньшие 7 (имеются в виду только целые неотрицательные числа).

3. Что можно сказать об истинности высказываний: «если аÎМ, то аÏ 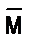», «если а делится на 3 и в не делится на 3, то а + в не делится на 3». Назовите простые высказывания, входящие в каждое из приведенных.

4. Являются ли высказываниями следующие записи: «3–2», «3<5», «таблицу умножения нужно знать наизусть», «а + 0 = а для любого натурального числа а»?