Отношение рода и вида между понятиями

Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» – родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник».

Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

В–третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Так как объем понятия – множество, удобно, устанавливая отношения между объемами понятий, изображать их при помощи кругов Эйлера.

А

В

Установим, например, отношения между следующими парами понятий а и b, если:

1) а – «прямоугольник», b- «ромб»;

Объемы понятий пересекаются, но не одно множество не является подмножеством другого. Следовательно, можно утверждать, что данные понятия а и b не находятся в отношении рода и вида.

А

В

2) а – «многоугольник», b – «параллелограмм»;

Объемы данных понятий находятся в отношении включения, но не совпадают – всякий параллелограмм является многоугольником, но не наоборот. Следовательно, можно утверждать, что понятие «параллелограмм» - видовое по отношению к понятию «многоугольник», а понятие «многоугольник» – родовое по отношению к понятию «параллелограмм».

А

В

3) а - «прямая», b – «отрезок».

Объемы понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком. Следовательно, данные понятия не находятся в отношении рода и вида.

О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок – часть прямой, а не ее вид.

Замечание.Если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого.

Например, отрезок не обладает такими свойствами прямой, как ее бесконечность.

3. Определение понятий

Появление в математике новых понятий, а значит, и новых терминов, обозначающих эти понятия, предполагает их определение.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). Как правило, делают это на основе ранее введенных понятий. Например, прямоугольник можно определить так: «Прямоугольником называется четырехугольник, у которого все углы прямые». В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через а первое понятие, а через b – второе, то данное определение можно представить в таком виде:

а есть (по определению) b

Слова «есть (по определению)» обычно заменяют символом 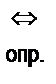, и тогда определение выглядит так: а 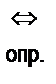b

Читают: «а равносильно b по определению». Можно прочитать эту запись еще и так: «а тогда и только тогда, когда b».

Определения, имеющие такую структуру, называются явными. Рассмотрим их подробнее.

Обратимся опять к определению прямоугольника, вернее, к его второй части – определяющему понятию. В нем можно выделить:

1) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник»,

2) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.

Определение. Видовое отличие – это свойства (одно или несколько), которые позволяют выделять определяемые объекты из объема родового понятия.

Итоги нашего анализа можно представить в виде схемы

Определяемое понятие

Родовое понятие

видовое отличие

+

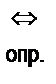Определяющее понятие

Заметим, что в наглядном представлении структуры определения через род и видовое отличие мы допустили некоторые неточности. Во–первых, слова «родовое понятие» означают, что речь идет о родовом понятии по отношению к определяемому. Во-вторых, не совсем ясно, что означает знак «+», который, как известно, используется для обозначения сложения чисел. Смысл этого знака станет понятным немного позже, когда мы рассмотрим математический смысл союза «и». А пока познакомимся с еще одной возможностью наглядного представления определения через род и видовое отличие. Если определяемое понятие обозначить буквой а, определяющее буквой b, родовое понятие (по отношению к определяемому) – буквой с, а видовое отличие – буквой Р, то определение через род и видовое отличие можно представить так:

а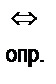

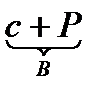
Почему видовое отличие обозначено заглавной буквой, мы узнаем позже.

Нам известно, что любое понятие имеет объем. Если понятие а определено через род и видовое отличие, то о его объеме – множестве А – можно сказать, что в нем содержатся такие объекты, которые принадлежат множеству С (объему родового понятия с) и обладают свойством Р: А= { х | хÎ С и Р (х)}.

Например, если дано определение: «Острым углом называется угол, который меньше прямого», - то объем понятия «острый угол» – это подмножество множества всех углов плоскости, которые обладают свойством «быть меньше прямого».

Так как определение понятия через род и видовое отличие является по существу условным соглашением о введении нового термина для замены какой – либо совокупности известных терминов, то об определении нельзя сказать, верное оно или неверное; его не доказывают и не опровергают. Но, формулируя определения, придерживаются ряда правил. Назовем основные.