Генерация простого числа

Для алгоритмов с открытыми ключами нужны простые числа. Их нужно множество для любой достаточно большой сети. Прежде, чем обсуждать математику генерации простого числа, я отвечу на несколько очевидных вопросов.

Если каждому понадобится свое простое число, не иссякнет ли у нас запас? Нет. В действительности существует приблизительно 10151 простых чисел длино1 до 512 бит включительно. Для чисел, близких n, вероятность того, что случайно выбранное число окажется простым, равна 1/ln n. Поэтому полное число простых чисел, меньших n, равно n/(ln n). Во вселенной всего 10⁷⁷ атомов. Если бы для каждого атома во вселенной с начала времен каждую микросекунду требовался бы миллиард простых чисел, понадобилось бы только 10¹⁰⁹ простых чисел, осталось бы еще примерно 10¹⁵¹ простых чисел.

Что если два человека случайно выберут одно и то же простое число? Этого не случится. При выборе из 10151 простых чисел вероятность совпадения выбора значительно меньше, чем вероятность, что ваш компьютер случайно вспыхнет в тот самый момент, когда вы выиграете в лотерею.

Если кто-то создаст базу данных всех простых чисел, не сможет ли он использовать эту базу данных для вскрытия алгоритмов с открытыми ключами? Нет. Если бы вы хранили один гигабайт информации на устройстве, весящем один грамм, то перечень простых чисел размером до 512 бит включительно весил бы столько, что масса хранилища превысила бы предел Чандрасекара, и оно сколлапсировало бы в черную дыру ... в любом случае вы не сможете извлечь данные.

Но если так трудоемко разложение на множители, как может быть простой генерация простых чисел? Фокус в том, что ответить "да" или "нет" на вопрос "Является ли число n простым?" гораздо проще, чем ответить на более сложный вопрос "Каковы множители n?"

Генерация случайных чисел с последующей попыткой разложения их на множители - это неправильный способ поиска простых чисел. Существуют различные вероятностные проверки на простоту чисел, определяющие, является ли число простым, с заданной степенью достоверности. При условии, что эта "степень достоверности" достаточна велика, такие способы проверки достаточно хороши. Я слышал, что простые числа, генерированные таким образом называются "промышленно простыми числами": эти числа вероятно являются простыми с контролируемой возможностью ошибки.

Предположим, что одна проверка из 2⁵⁰ - ошибочна. Это означает, что с вероятностью 1/10¹⁵ проверка объявит простым составное число. (Простое число никогда не будет объявлено составным при проверке.) Если по какой-то причине понадобится большая достоверность простоты числа, уровень ошибки можно понизить. С другой стороны, если вы установите вероятность того, что число является составным, в 300 миллионов раз меньшей, чем вероятность выиграть главный приз в государственной лотерее, вы можете больше об этом не волноваться.

Обзоры недавних исследований в этой области можно найти в [1256, 206]. Другими важными работами являются [1490, 384, 11, 19, 626, 651, 911].

Solovay-Strassen

Роберт Соловэй (Robert Solovay) и Фолькер Штрассен (Volker Strassen) разработали алгоритм вероятностной проверки простоты числа [1490]. Для проверки простоты числа p этот алгоритм использует символ Якоби:

(1) Выберите случайно число a, меньшее p.

(2) Если НОД(a,p) (1, то p не проходит проверку и является составным.

(3) Вычислите j = a(p-1)/2 mod p.

(4) Вычислите символ Якоби J(a,p).

(5) Если j ¹ J(a,p), то число p наверняка не является простым.

(6) Если j = J(a,p), то вероятность того, что число p не является простым, не больше 50 процентов.

Число a, которое не показывает, что p наверняка не является простым числом, называется свидетелем. Если p - составное число, вероятность случайного числа a быть свидетелем не ниже 50 процентов. Повторите эту проверку t раз с t различными значениями a. Вероятность того, что составное число преодолеет все t проверок, не превышает 1/2^t.

Lehmann

Другой, более простой тест был независимо разработан Леманном (Lehmann) [903]. Вот последовательность действий при проверке простоты числа p:

(1) Выберите случайно число a, меньшее p.

(2) Вычислите a^(p-1)/2 mod p.

(3) Если a^(p-1)/2 ¹ 1 или -1 (mod p), то p не является простым.

(4) Если a^(p-1)/2 º 1 или -1 (mod p), то вероятность того, что число p не является простым, не больше 50 процентов.

И снова, вероятность того, что случайное число a будет свидетелем составной природы числа p, не меньше 50 процентов. Повторите эту проверку t раз. Если результат вычислений равен 1 или -1, но не всегда равен 1, то p является простым числом с вероятностью ошибки 1/^2t.

Rabin-Miller

Повсеместно используемым является простой алгоритм, разработанный Майклом Рабином (Michael Rabin), частично основанным на идеях Гэри Миллера [1093, 1284]. По сути, это упрощенная версия алгоритма, рекомендованного в предложении DSS proposal [1149, 1154].

Выберите для проверки случайное число p. Вычислите b - число делений p - 1 на 2 (т.е., 2^b - это наибольшая степень числа 2, на которое делится p - 1). Затем вычислите m, такое что p = 1 + 2^b * m.

(1) Выберите случайное число a, меньшее p.

(2) Установите j = 0 и z = am mod p.

(3) Если z = 1 или если z = p - 1, то p проходит проверку и может быть простым числом.

(4) Если j > 0 и z = 1, то p не является простым числом.

(5) Установите j = j + 1. Если j < b и z( p - 1, установите z = z² mod p и вернитесь на этап (4). Если z = p - 1, то p проходит проверку и может быть простым числом.

(6) Если j = b и z ¹ p - 1, то p не является простым числом.

В этом тесте вероятность прохождения проверки составным числом убывает быстрее, чем в предыдущих. Гарантируется, что три четверти возможных значений a окажутся свидетелями. Это означает, что составное число проскользнет через t проверок с вероятностью не большей (1/4)^t, где t - это число итераций. На самом деле и эти оценки слишком пессимистичны. Для большинства случайных чисел около 99.9 процентов возможных значений a являются свидетелями [96].

Существуют более точные оценки [417]. Для n-битового кандидата в простые числа (где n больше 100), вероятность ошибки в одном тесте меньше, чем 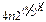. И для 256-битового n вероятность ошибки в шести тестах меньше, чем 1/2⁵¹. Дополнительную теорию можно найти в [418].