ПЕРЕХОД К САМОТЕСТИРОВАНИЮ
| предыдущая глава | содержание | следующая глава |
| предыдущая глава | содержание | следующая глава |
ГЛАВА 18. ОЦЕНКА И АНАЛИЗ ТОЧНОСТИ СЧИСЛЕНИЯ КООРДИНАТ СУДНА
18.1. Погрешности измерений и их виды
В процессе определения значения навигационного параметра участвуют:
1. → оператор (наблюдатель), производящий измерения и вычисления;
2. → приборы и инструменты, с помощью которых производятся измерения.
Результаты измерений (их точность) будут зависеть, прежде всего, от:
1. → навыков и психофизического состояния оператора (наблюдателя);
2. → технического состояния измерительных приборов и инструментов;
3. → характера объекта измерений (отчетливо виден, сливается с фоном);
4. → условий внешней среды (плохая видимость, сильная качка и т.д.);
5. → от знания значений поправок приборов (инструментов).
Вполне очевидно, что чем полнее будут учтены все факторы, влияющие на измеренный навигационный параметр, тем точнее будет и результат измерений.
Практически невозможно учесть все факторы, которые влияют на точность измерений.
Поэтому, измеренный и исправленный всеми поправками навигационный параметр (Ui), будет отличаться от истинного его значения (U0) на величину абсолютной погрешности (Δ), то есть:
| Δ = Ui − U0 | (18.1) |
Абсолютной или истинной погрешностью измерения (Δ) называется разность между измеренным (Ui) и истинным (U0) значениями навигационного параметра.
Истинное значение навигационного параметра на момент его измерения может быть известно только в определенных случаях и то с какой-то вероятностью.
В большинстве же случаев штурманской практики погрешность измерения рассчитывают относительно вероятнейшего (среднего арифметического) значения измеренного навигационного параметра, то есть
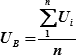
| (18.2) |
| где | 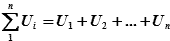 – сумма всех значений навигационного параметра в данной серии его измерения; – сумма всех значений навигационного параметра в данной серии его измерения;
|
| n – число измерений навигационного параметра в серии. |
Имея вероятнейшее (среднее арифметическое) значение навигационного параметра можно рассчитать погрешность каждого его измерения.
Погрешностью измерения или отклонением измерения от вероятнейшего значения измеряемого навигационного параметра (υ) называют разность между измеренным, исправленным всеми поправками и приведенным к одному моменту и месту значением навигационного параметра (Ui) и его вероятнейшим (UB) значением, то есть:
| υ = Ui − UB | (18.3) |
Теперь можно сказать, что любой измеренный навигационный параметр есть величина случайная и лишь с какой-то степенью достоверности соответствующая его истинному (U0) или вероятнейшему (UB) значению.
Все погрешности измерений делятся на 3 вида:
1. случайные; 2. систематические; 3. грубые (промахи).
| I. | Случайные погрешности – это погрешности, величина и знак которых случайно изменяются от измерения к измерению одного и того же навигационного параметра в данном комплексе измерений (рассеивание пуль при стрельбе по мишени, «разброс» пеленгов при пеленговании ориентира и др.). |
Появление и величина случайных погрешностей зависит от опыта наблюдателя, от качества измерительных приборов и от условий измерения навигационного параметра.
Случайные погрешности обладают следующими основными свойствами:
1. → вероятнейшее значение измеряемого навигационного параметра (UB) приближается к истинному его значению (U0) по мере увеличения количества его измерений (n);
2. → появление случайных погрешностей равных по величине, но противоположных по знаку равновероятно (свойство симметрии);
3. → при увеличении числа измерений (n) навигационного параметра средняя арифметическая погрешность (υСР) стремится к «нулю»: ( 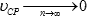 );
);
4. → большие по величине случайные погрешности менее вероятны, чем малые.
Неоднократные измерения одного и того же навигационного параметра (>3÷5 раз) и расчет среднего его значения в какой-то мере исключают влияние на конечный результат случайных погрешностей.
| II. | Систематические погрешности – это погрешности, которые сохраняют свой знак и величину при каждом измерении навигационного параметра или закономерно изменяются по определенному закону с изменением условий измерений (неверно определена ΔК, ΔЛ% и пр.), что одинаково будет влиять на значение каждого измерения). |
Появление и величина систематических погрешностей зависит от точности работы наблюдателя и правильного учета поправок приборов и инструментов, с помощью которых измеряются, вычисляются и прокладываются на карте значения навигационного параметра (ИК, ИП, ПУ, SЛ и пр.).
Важнейшим свойством систематических погрешностей является постоянство знака и величины погрешности или конкретная определенность в характере изменения этой погрешности с течением времени.
На основании этого свойства систематические погрешности могут и должны быть определены, а затем и максимально исключены из результатов измерения навигационного параметра.
| III. | Грубые погрешности (промахи) – это случайные погрешности, значения которых превышают по величине допустимые пределы точности для данного вида наблюдений. Такие погрешности возникают из-за значительных нарушений правил измерения и обработки, невнимательности наблюдателя и пр. |
Измерение с промахом считается недействительным и исключается из общей серии измерений.
Если систематические и грубые погрешности можно уменьшить или исключить из результатов измерений навигационного параметра, то выявить и учесть случайные погрешности невозможно и именно они преобладают во всех измерениях.
Случайные погрешности можно учесть только в среднем, а для этого надо знать и применять законы, которым подчиняются эти погрешности и улучшать условия, в которых проводятся измерения.
Основным математическим законом, которому подчиняются случайные погрешности является закон нормального распределения случайных погрешностей (закон Гаусса Карла Фридриха (1775÷1855)) – рис. 18.1.
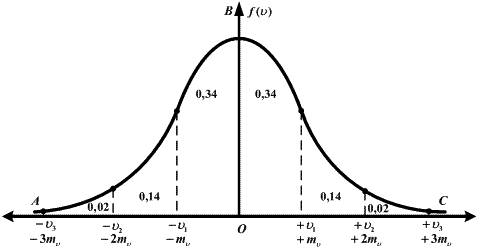
Рис. 18.1. Закон нормального распределения случайных погрешностей
Исследуя кривую погрешностей (палатка Эйлера, кривая Гаусса, нормальная кривая вероятностей) можно сделать следующие выводы:
1. → положительные и отрицательные погрешности равновероятны;
2. → положительные и отрицательные погрешности одной и той же абсолютной величины равновероятны;
3. → погрешности, малые по своей абсолютной величине, более вероятны, чем погрешности большие;
4. → по мере роста величин случайных погрешностей их вероятности уменьшаются и приближаются к нулю, но никогда его не достигают;
5. → теоретически не исключается возможность получения бесконечно больших погрешностей (кривая не пересекает ось абсцисс).
В законе нормального распределения случайных погрешностей основной характеристикой оценки точности измерения навигационного параметра является средняя квадратическая погрешность (СКП) – это среднее квадратическое отклонение измеренного навигационного параметра (Ui) от вероятнейшего его значения (UB).
Значение СКП измерения навигационного параметра можно рассчитать по формуле:
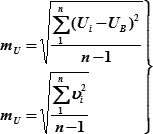
| (18.4) |
На практике СКП измерения любого навигационного параметра рассчитывается двумя способами:
1. → по отклонениям от среднего арифметического (ф. 18.4);
2. → по «размаху» измерений (менее точный).
Вероятность того, что погрешность навигационного параметра (Ui) не превосходит его СКП (mU), равна 0,68 или 68% (рис. 18.1).
Предельную погрешность ( 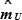 ) измерения навигационного параметра в зависимости от заданной ее вероятности (Р) рассчитывают по формуле:
) измерения навигационного параметра в зависимости от заданной ее вероятности (Р) рассчитывают по формуле:
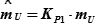
| (18.5) |
| где | КР1 – коэффициент по заданной вероятности (см. табл. 1б «МТ-75» (с. 61) или табл. 4.7 «МТ-2000» (с. 395) «Функция Лапласа»), |
то есть:
| 1) | для Р = 95,4% | 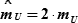
| (КР1 = Z = 2,0); |
| 2) | для Р = 98,8% | 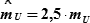
| (КР1 = Z = 2,5); |
| 3) | для Р = 99,7% | 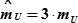
| (КР1 = Z = 3,0); |
| 4) | для Р = 99,9% | 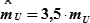
| (КР1 = Z = 3,5). |
Функция Лапласа
(из табл. 1б «МТ-75» или табл. 4.7. «МТ-2000»)
Таблица 18.1
| Z | ||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 3,0 3,5 | 0,000 080 158 236 311 0,383 452 516 576 632 0,683 729 770 806 838 0,866 890 911 928 943 0,954 964 972 979 984 0,988997 1,000 | 0,008 088 166 243 318 0,390 458 522 582 637 0,688 733 774 810 842 0,869 893 913 930 944 0,956 965 973 979 984 0,988 997 1,000 | 0,016 095 174 251 325 0,397 465 528 588 642 0,692 737 777 813 844 0,871 895 915 931 945 0,957 966 974 980 984 0,988 997 1,000 | 0,024 103 182 259 333 0,404 471 535 594 648 0,697 742 781 816 847 0,874 897 916 933 946 0,958 967 974 980 985 0,989 998 1,000 | 0,032 111 190 266 340 0,411 478 541 599 653 0,702 746 785 820 850 0,876 899 918 934 948 0,959 968 975 981 985 0,989 998 1,000 | 0,040 119 197 274 347 0,418 484 547 605 658 0,706 750 789 823 853 0,879 901 920 936 949 0,960 968 976 981 986 0,989 998 1,000 | 0,048 127 205 281 354 0,424 491 553 610 663 0,711 754 792 826 856 0,881 903 922 937 950 0,961 969 976 982 986 0,990 998 1,000 | 0,056 135 213 289 362 0,431 497 559 616 668 0,715 758 796 829 858 0,884 905 923 938 951 0,962 970 977 982 986 0,990 998 1,000 | 0,064 143 221 296 369 0,438 504 564 621 673 0,720 762 799 832 861 0,886 907 925 940 952 0,962 971 977 983 987 0,990 998 1,000 | 0,072 151 228 304 376 0,445 510 570 626 678 0,724 766 803 836 864 0,888 909 927 941 953 0,963 972 978 983 987 0,990 998 1,000 |
Вероятность нахождения нормальной случайной величины (Х) в интервале от «α» до «δ» определяется по формуле:
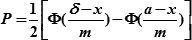
| (18.6) |
| Задача 1: | Определить вероятность измерения расстояния с погрешностью, не превосходящей по абсолютной величине 150м, если систематическая погрешность измерения расстояния равна 50м в сторону уменьшения расстояния. Случайные погрешности подчиняются нормальному закону и имеют СКП m = 100м. |
| Решение: | 1) По ф. 18.6: 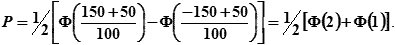 2) Из табл. 18.1: Ф(2) = 0,954, Ф(1) = 0,683 3) 2) Из табл. 18.1: Ф(2) = 0,954, Ф(1) = 0,683 3) 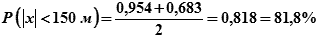
|
| Задача 2: | Рассчитать погрешность в измерении пеленга (υn), соответствующую Р = 95%, если СКП измерения пеленга m°n = ±0,3°. |
| Решение: | 1) Из табл. 18.1. обратным входом по Р = 0,95 выбираем величину Z = 1,96. 2) Рассчитываем υn = 1,96 · 0,3° ≈ ± 0,6°. |
| Задача 3: | Определить вероятность появления погрешности в пеленге, не превышающей ±0,5°, если СКП компасного пеленга m = ±0,2° |
| Решение: | 1) Вычисляем 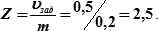 2) Из табл. 18.1 по аргументу Z = 2,5 находим искомую вероятность Р = 0,988. 2) Из табл. 18.1 по аргументу Z = 2,5 находим искомую вероятность Р = 0,988.
|
| Задача 4: | Определить пределы, в которых находится погрешность измерения расстояния с Рзад = 0,866, если СКП измерения расстояния mD = ±0,5 кб. |
| Решение: | 1) Из табл. 18.1 по аргументу Р = 0,866 определяем Z = 1,5. 2) Вычисляем искомые пределы погрешности υD = 1,5 · 0,5 = ±0,75кб. |
| Задача 5: | Определить вероятность того, что действительное расстояние до ориентира не выйдет за пределы 105÷108кб, если среднее арифметическое (вероятнейшее) расстояние до ориентира D = 106кб., а СКП измерения расстояния mD = ±2 кб. |
| Решение: | 1) Рассчитываем аргументы функции Лапласа для случайных величин: 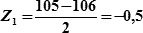 и и 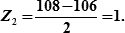 2) Из табл.18.1 по аргументам Z1 и Z2 выбираем значения вероятностей: Р1 = 0,383 и Р2 = 0,683 3) Вычисляем искомую вероятность Р = 0,5 (0,683 + 0,383) = 0,533. (т.к. «Z1» величина отрицательная, то функции Лапласа складываются). 2) Из табл.18.1 по аргументам Z1 и Z2 выбираем значения вероятностей: Р1 = 0,383 и Р2 = 0,683 3) Вычисляем искомую вероятность Р = 0,5 (0,683 + 0,383) = 0,533. (т.к. «Z1» величина отрицательная, то функции Лапласа складываются).
|
Дата добавления: 2021-01-26; просмотров: 546;











