Оценка точности счисления координат судна

Современный уровень штурманской техники все еще не позволяет перейти к обсервационному способу судовождения, то есть судовождению на основе непрерывного определения места судна по внешним ориентирам. Поэтому основой выработки текущих (счислимых) координат места судна является счисление его пути, на основе которого получают (графически, аналитически, графо-аналитически) текущие координаты (счислимое место судна) на любой момент времени.

Счислимое место судна на любой момент времени определяется точкой пересечения двух линий (рис. 18.2.):

• линии пути судна;
• дуги окружности, проведенной из исходной точки плавания, радиусом, равным пройденному судном расстоянию.

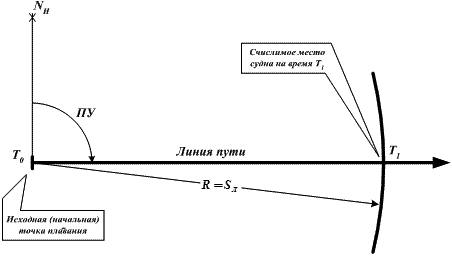
Рис. 18.2. Счислимое место судна

В результате неточного учета (или их изменения со временем) таких элементов, как поправка курсоуказателя (ΔК), величина угла дрейфа (α°), направление учитываемого течения (К_Т) и его скорости (υ_Т) и пр. – путевой угол (ПУ) будет отличаться от расчетного на некоторую величину (ΔПУ).

В результате же неточного учета (или их изменения со временем) таких элементов, как поправка лага (ΔЛ%), скорость учитываемого течения (υ_Т) и пр. – пройденное судном расстояние (S_Л) будет отличаться от расчетного на некоторую величину (ΔS).

Учтя все погрешности, влияющие на путевой угол и все погрешности, влияющие на пройденное судном расстояние (см. табл. 12.1.), можно получить СКП путевого угла (m_ПУ) и СКП пройденного судном расстояния (m_S).

Под воздействием этих погрешностей (m_ПУ и m_S) счислимое место судна на какой-то момент времени Т₁ (рис. 18.3) будет располагаться не в конкретной точке (т. а), а в пределах некоторой площади (на рис. 18.3 – заштриховано), но где именно – заранее не известно.

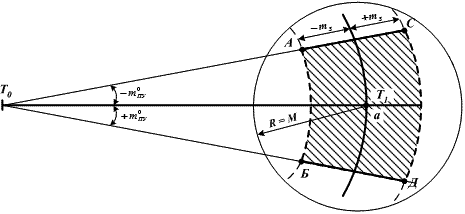
Рис. 18.3. Погрешность счисления пути судна

Это объясняется тем, что величина и знак абсолютного изменения путевого угла (ΔПУ) и пройденного расстояния (ΔS) проявляются как случайные величины.

Ссылаясь на теорию погрешности можно оценить вероятность нахождения счислимого места на время Т₁ в «заштрихованной» (рис. 18.3) фигуре погрешности величиной Р = 46% (0,46).

Если в эту фигуру вписать эллипс на полуосях

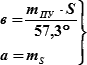
(18.7)

то вероятность нахождения счислимого места на время Т₁ в эллипсе оценится в Р ≈ 39% (0,39). → рис. 18.11.

В практике судовождения точность места принято оценивать радиальной или круговой среднеквадратической погрешностью

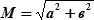
(18.8)

Зная значение М из т. а проведем окружность радиусом R = М. Вероятность нахождения счислимого места в круге, радиусом R = M, составит 63÷68% (0,63÷0,68) в зависимости от соотношения полуосей эллипса (а и в).

Как видно из рис. 18.3 величина радиуса R = M будет увеличиваться постоянно с увеличением пройденного судном расстояния (S).

На основании многолетних наблюдений получены следующие приближенные значения радиуса R = M для нормальных условий плавания в зависимости от пройденного расстояния:

• без ветра и течения: М ≈ 0,02·S → если S = 100 миль, то М = 2 мили;
• с учетом дрейфа от ветра: М ≈ 0,03·S → если S = 100 миль, то М = 3 мили;
• с учетом дрейфа от ветра и течения: М ≈ 0,03÷0,07·S → если S = 100 миль, то М = 3÷7 миль.

Для конкретного проекта (типа) судна для конкретного района плавания (Черное море, Средиземное море и др.) нужно знать значение радиальной СКП счисления (М_С), чтобы иметь возможность в любое время оценить навигационную безопасность плавания.

Величина М_С зависит от пройденного судном расстояния, то есть от времени плавания по счислению. Осталось выяснить «скорость» увеличения М_С, то есть знать величину – коэффициента точности счисления (К_С).

Вероятность радиальной погрешности
(из табл. 1в «МТ-75» и табл. 4.13 «МТ-2000»)

Таблица 18.2.

КР =	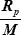Отношение полуосей эллипса погрешностей е = в/а
0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0	0,080 159 236 311 383 452 516 576 632 0,683 729 770 806 838 866 890 911 928 943 0,954 964 972 979 984 988 991 993 995 996 0,997	0,045 135 223 303 377 448 514 575 631 0,683 729 771 807 840 868 891 912 929 944 0,955 965 973 979 984 988 991 993 995 996 0,997	0,025 092 179 270 356 434 505 570 629 0,682 730 772 810 842 870 895 915 932 946 0,958 967 975 981 985 989 992 994 996 997 0,998	0,018 068 142 229 319 406 486 558 623 0,680 731 775 814 847 875 899 919 936 950 0,961 970 977 983 987 990 993 995 996 997 0,998	0,014 056 119 198 285 374 459 539 610 0,674 729 776 817 852 881 905 925 942 955 0,965 974 980 985 989 992 994 996 997 998 0,999	0,012 048 105 177 260 347 434 517 594 0,663 723 775 819 856 886 911 931 947 960 0,970 978 984 988 991 994 996 997 998 999 0,999	0,011 044 096 164 243 328 415 499 579 0,652 716 772 819 858 890 916 936 952 965 0,974 981 987 990 993 995 997 998 999 999 0,999	0,011 042 091 156 232 315 401 487 568 0,643 710 768 818 859 892 919 940 956 968 0,978 984 989 992 995 997 998 999 999 999 1,000	0,010 040 088 151 225 307 393 478 560 0,636 705 765 817 859 894 921 943 959 971 0,980 986 991 994 996 998 998 999 999 1,000 1,000	0,010 039 086 149 222 304 389 474 556 0,633 703 764 816 859 894 922 944 960 972 0,981 987 992 995 997 998 999 999 999 1,000 1,000	0,010 039 086 148 221 302 387 473 555 0,632 702 763 815 859 895 923 944 961 973 0,982 988 992 995 997 998 999 999 1,000 1,000 1,000

К_Р = R_Р / М → коэффициент (нормированная радиальная погрешность), равный заданной радиальной погрешности (R_Р) в долях радиальной СКП места (М).

Если «а» и «в» неизвестны, то выборки по в/а = 1.

Задача:	Определить вероятность нахождения места судна в круге радиуса 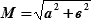и круге радиуса RР = 2,9 мили, если полуоси эллипса погрешностей: а = 1,8 мили, в = 0,7 мили.
Решение:	1) рассчитываем отношение полуосей эллипса: e = b/a = 0,7/1,8 = 0,4. 2) вычисляем радиальную СКП места судна: 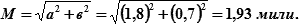3) из табл. 18.2 по КР = 1 (для радиальной СКП RР = М) и е = 0,4 выбираем Р = 0,674 (67,4%) 4) из табл. 18.2 по 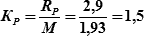и е = 0,4 выбираем Р = 0,881 (88,1%).

Вероятность радиальной погрешности при круговом распределении мест
(из табл. 4.15 «МТ-2000»)

Таблица 18.3.

КР =	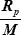0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8	0,010 039 086 148 221 302 387 473 555 0,632 702 763 815 859 895 923 944 961 973 0,982 988 992 995 997 998 999 999 1,000	0,012 043 092 155 229 311 396 481 563 0,639 708 769 820 863 898 925 946 962 974 0,982 988 992 995 997 998 999 999 1,000	0,014 047 097 162 237 319 405 490 571 0,647 715 774 825 867 901 928 948 964 975 0,983 989 993 995 997 998 999 999 1,000	0,017 052 103 169 245 328 413 499 579 0,654 721 780 829 871 904 930 950 965 976 0,984 989 993 996 997 998 999 999 1,000	0,019 056 109 176 253 336 422 506 587 0,661 727 785 834 874 907 932 952 966 977 0,984 990 993 996 997 998 999 999 1,000	0,022 061 115 183 261 345 430 514 594 0,668 734 790 838 878 910 934 953 968 978 0,985 990 994 996 998 998 999 999 1,000	0,025 065 122 191 269 353 439 523 602 0,675 740 796 843 881 912 936 955 969 979 0,986 991 994 996 998 999 999 1,000 1,000	0,028 070 128 198 277 362 447 531 610 0,682 746 801 847 885 915 939 956 970 979 0,986 991 994 996 998 999 999 1,000 1,000	0,032 075 134 206 286 370 456 539 617 0,689 752 806 851 888 918 941 958 971 980 0,987 991 994 997 998 999 999 1,000 1,000	0,035 081 141 213 294 379 464 547 625 0,695 757 811 855 891 920 943 959 972 981 0,987 992 995 997 998 999 999 1,000 1,000

К_Р = 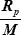– отношение заданной радиальной погрешности (R_Р) к радиальной СКП места (М) при b/a = 1.

Задача 1:	Определить вероятность нахождения действительного места судна в круге радиуса RР = 1,2 мили, если радиальная СКП при круговом распределении мест судна М = 0,6 мили.
Решение:	из табл. 18.3 по коэффициенту 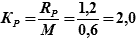выбираем значение Р = 0,982 (98,2%).
Задача 2:	Определить радиальную погрешность для вероятности Рзад = 0,95 (95%), если радиальная СКП при круговом распределении мест судна М = 0,8 мили.
Решение:	из табл. 18.3 по Рзад = 0,95 (95%) выбираем КР = 1,73 следовательно: R0,95 = 1,73 · 0,8 мили = 1,4 мили.