Другие виды зацепления

Помимо эвольвентного зацепления ограниченное распространение получили и другие виды зацепления. В прошлом было широко распространено циклоидальное (циклоидное) зацепление. Если чертящую точку взять не на прямой, а на производящей окружности, и перекатывать ее по основной окружности, чертящая точка будет описывать кривую, называемую циклоидой. Причем, если производящая окружность катится снаружи основной, будет эпициклоида, если внутри – гипоциклоида. В циклоидальном зубчатом колесе профиль головки зуба выполняется по эпициклоиде, а профиль ножки зуба – по гипоциклоиде. Преимущество циклоидального зацепления – контакт выпукло- вогнутых поверхностей и, как следствие, уменьшение контактных напряжений. Недостаток – нельзя изменять межцентровое расстояние и вообще менять колеса в парах.

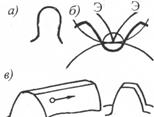
Рис. 5.20. Другие виды зацеплений: циклоидное -а, цевочное –б, зацепление Новикова -в

Разновидностью циклоидального является часовое зацепление, в этом зацеплении эпициклоида головки зуба заменена дугой окружности, а гипоциклоида – прямой (циклоида превращается в прямую, если r_n = 0.5 r_b (рис. 5.20)). Достоинства зацепления, большие передаточные отношения и уменьшенный износ по сравнению с эвольвентным зацеплением.

Другой разновидностью циклоидального зацепления является цевочное зацепление. Боковой профиль зуба шестерни выполняется по эпициклоиде, зуб другого колеса - в виде цилиндрического ролика, называемого цевкой (рис. 5.20,б). При соответствующем выборе параметров профили будут сопряженными. Такое зацепление применяется там, где большое колесо по технологическим соображениям выполнить невозможно, его собирают из дисков, снабженных цевками. Такие колеса применяются, например, для привода поворотных платформ больших экскаваторов.

Циклоидно-цевочное зацепление имеет ряд преимуцществ по сравнению с эвольвентным зацеплением, но оно достаточно сложно в технологическом отношении . В настоящее время получают распространени планетарные редукторы с таким видом зацепления.

Сравнительно недавно было предложено круговинтовое зацепление (зацепление Новикова). Если в обычном эвольвентном зацеплении зубья касаются по контактной линии, которая перемещается по высоте зуба, то в круговинтовом зацеплении контакт происходит в точке, которая перемещается вдоль зуба. В качестве профилей зубьев здесь используются дуги окружностей (рис. 5.20, в). Так как разница радиусов кривизны невелика, контактные напряжения малы. Поскольку точка контакта перемещается вдоль зуба, высоту зуба можно делать небольшой, тем самым, увеличивая прочность зубьев. Зубчатые колеса с круговинтовыми зубьями, несмотря на их достоинства, нашли ограниченное применение в связи со сложностью изготовления инструмента для их нарезки.

5.20. Пространственные зубчатые передачи

Винтовая передача – передача между цилиндрическими колесами со скрещивающимися осями. (рис. 5.21,а). Передача образована обычными косозубыми колесами, у которых углы наклона зубьев β₁ и β₂ и угол скрещивания осей β находятся в соотношении β = β₁ + β₂.

Здесь имеет место точечное касание, что является недостатком передачи. Передаточное отношение колеблется в пределах 1 - 5. При передаточном отношении U ≥ 5 винтовая передача переходит в червячную (рис.5.21,б).

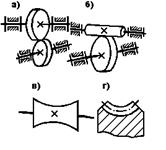
Рис. 5.21. Винтовая и червячная передачи

Червячные передачи находят широкое применение в технике. Ее достоинства – большое передаточное отношение, плавность, бесшумность, в большинстве случаев свойство самоторможения. Недостатки – низкий к.п.д., большие осевые усилия на подшипники, повышенный износ червячного колеса.

Червяк представляет собой винтовое зубчатое колесо малого диаметра и большой ширины, с большим наклоном зуба червяка, как и винты, могут быть одно- и многозаходными. Под числом заходов понимается число зубьев червяка. Червячное колесо представляет косозубое эвольвентное колесо с углом наклона зуба β = 90˚ - γ, где γ – угол подъема винтовой линии на делительной окружности червяка. Для повышения долговечности передач, улучшения смазки колеса делают не цилиндрическими и придают им специальную форму. Червяк делают глобоидным (рис. 5.21, в), червячному колесу придают форму, показанную на рис. 5.21,г.

Передаточное отношение червячной передачи определяется по формуле:

i = Z_к / Z_ч, (5.9)

где Z_к - число зубьев колеса, Z_ч – число зубьев (заходов) червяка.

Для однозаходного червяка передаточное отношение равно числу зубьев червячного колеса, что и объясняет большое передаточное отношение червячных передач.

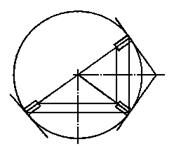
Рис. 5.22. Коническая передача

Коническая передача образована коническими зубчатыми колесами с пересекающимися осями (рис. 5.22). В основе передачи лежат начальные конусы, перекатывающиеся друг по другу без скольжения. Часть зуба, выступающая за начальный конус, является головкой, а часть, лежащая внутри – ножкой зуба. Высота головки и ножки, а также остальные размеры зубьев, в том числе и модуль, уменьшаются при переходе от наружного торца колеса к внутреннему.

За модуль колеса принимается наибольший, относящийся к делительной окружности наружного торца колеса. Размеры зубьев подсчитываются по тем же формулам, что и для прямозубых колес. Нарезание конических колес с прямыми зубьями возможно только на специальных зубострогальных станках. Применяются также конические колеса с криволинейными зубьями.

5.21. Передаточное отношение и передаточное число

Важнейшей характеристикой всякого зубчатого механизма является передаточное отношение.

Передаточным отношением зубчатой передачи называется отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого зубчатого колеса (ГОСТ 16530-83). Передаточное отношение принято обозначать буквой i.

Понятие передаточного отношения для зубчатого механизма стандартом не определено, поэтому обычно пользуются общепринятым определением аналогичным передаточному отношению зубчатой передачи: передаточное отношение зубчатого механизма есть отношение угловых скоростей звеньев. Передаточное отношение принято снабжать индексвами, указывающими номера зубчатых колес, например, i₁₂ = ω₁/ω₂. Из рассмотрения зубчатой передачи на рис.5.23 следует:

V_A1 = ω₁ r₁ ; V_A2 = ω₂ r₂; V_A1 = V _A2.

Тогда

i₁₂ = ω₁ / ω₂ = r₂ / r₁ = m z₂ / m z₁ = z₂ / z₁. (5.10)

Передаточному отношению присваивается знак +, если входное и выходное колеса вращаются в одном направлении, и знак -, если они вращаются в разном направлении. Для зубчатой передачи внешнего зацепления передаточное отношение i₁₂ отрицательно, для внутреннего зацепления – положительно. При передаточном отношении больше единицы имеем редуктор (замедление скорости), при передаточном отношении меньше единицы – мультипликатор (происходит увеличение скорости вращения).

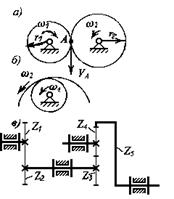
Рис. 5.23. Зубчатая передача внешнего и внутреннего

зацепления и рядовой зубчатый механизм

В подавляющем большинстве случаев механизмы являются редукторами. Их назначение – уменьшать частоту вращения двигателя до той, которая необходима для нормальной работы исполнительного органа машины. Одновременно с уменьшением частоты вращения повышается крутящий момент. Так как к.п.д. зубчатой передачи очень высок (0.95 – 0.98), то можно считать, что мощности N₁ = N₂, где N₁ = M₁ ω_1, N₂ = M₂ ω₂, отсюда следует, что M₂ = M₁ i₁₂.

Передаточное отношение не следует путать с передаточным числом, под которым понимается отношение угловой скорости большего колеса к угловой скорости меньшего, называемого обычно шестерней. Передаточное число всегда больше единицы и знака не имеет.

Рядовой зубчатой передачей (зубчатым рядом) называется зубчатый механизм, образованный зубчатыми колесами с неподвижными осями. Зубчатый ряд состоит из одной или нескольких зубчатых передач. Рассмотрим механизм на рис. 5.24. Он составлен из трех зубчатых передач, образованных колесами z₁, z₂, z₃, z₄, z₅, z₆. Запишем их передаточные отношения:

i₁₂ = ω₁./ ω₂; i₃₄ = ω₃ / ω₄; i₄₅ = ω₄ / ω_5,

откуда

ω₂ = ω₁ / i₁₂; ω₄ = ω₃ /i₃₄; ω₅ = ω₄ / i₄₅.

Производя последовательную подстановку выражений для ω₂, ω₄, ω₅, получим

ω₅ = ω₁ / i₄₅ i₃₄ i₁₂,

откуда

i₁₅ = i₁₂ i₃₄ i₄₅.

Полученная формула является частным случаем общего правила, формулируемого следующим образом:

Передаточное отношение рядовой зубчатой передачи равно произведению передаточных отношений входящих в нее зубчатых передач, при этом следует учитывать знаки передаточных отношений составляющих зубчатых передач.

Передаточное отношение также можно выразить через числа зубьев:

i₁₅ = Z₂ Z₄Z₅ / Z₁ Z₂ Z₄. (5.11)

Полученная формула является частным случаем общего правила , формулируемого следующим образом:

передаточное отношение рядовой зубчатой передачи равно дроби, в числителе которой стоят числа зубьев выходных колес, а в знаменателе – входных. Знак берется согласно указанному выше правилу знаков. В формуле колесо Z₄ не влияет на численное значение передаточного отношения, но влияет на знак. Такое колесо называется паразитным.

5.22. Расчёт рядовой коробки передач

В качестве примера рассмотрим коробку передач легкового автомобиля, в основе которой рядовой зубчатый механизм (рис. 5.24).

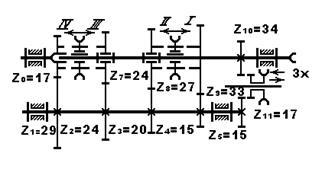
Рис. 5.24. Коробка передач автомобиля

Она состоит из входного вала 1, выходного вала 2 и промежуточного вала 3. На промежуточном валу жестко закреплены колеса с числом зубьев Z₁ = 29, Z₂ = 24, Z₃ = 20, Z₄ = 15, Z₅ = 15, на входном валу – колесо Z₆ = 17. На выходном валу подвижно установлены колеса Z₇ = 24, Z₈ = 27, Z₉ = 33.

Для включения передачи 1 рычагом переключения передач передвигается кулачковая муфта М₁ направо так, что она кулачками сцепляется с колесом Z₉. Передвигая муфту влево, включаем передачу II, аналогично посредством муфты М₂ происходит включение передач III IY. При указанных числах зубьев колес рассчитаем передаточные отношения на I ,II, IIIиIY передачах:

i^I = 29 33 / 17 15 = 3.75,

i^II ₌ 29 27 / 17 20 = 2.303,

i^III = 29 21/ 17 24 = 1.49,

i^IY = 1.

Вводя в зацепление с колесами Z₅=15 и Z₁₀ = 34 паразитное колесо Z₁₁, получаем передачу заднего хода с передаточным отношением

i_зх = - 29• 34 / 17 •15 = - 3.88.

5.23. Планетарные зубчатые механизмы

Планетарным называется зубчатый механизм, содержащий колеса с подвижными осями. Планетарные зубчатые механизмы широко распространены в технике, особенно транспортной, так как, обладая большим передаточным отношением, имеют малые габариты и вес. Иногда эти механизмы называют эпициклическими, так как траектории точек колес с подвижными осями при внешнем зацеплении представляют эпициклоиды. Простейший планетарный механизм представлен на рис. 5.25. Колесо 2 с подвижной осью называется сателлитом, центральное колесо 1 – солнечным, звено, несущее ось сателлита, называется водилом, его принято обозначать буквой Н.

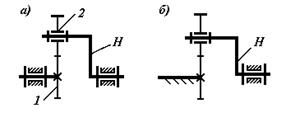
Рис. 5.25. Схема простейшего планетарного механизма

Если колесо 1 подвижно, степень подвижности механизма, рассчитанная по формуле Чебышева, равна 2, Если остановить колесо 1, получим механизм с W = 1 (рис. 5.25,б) Механизмы, у которых W>1, называются дифференциальными (зубчатыми дифференциальными). Если у планетарного механизма остановить водило, оставив колеса свободными, получим рядовую передачу.

Схема планетарных механизмов могут быть очень разнообразными. Практическое применение нашло, в основном, только несколько схем. Наиболее распространенные схемы представлены на рис. 5.26.

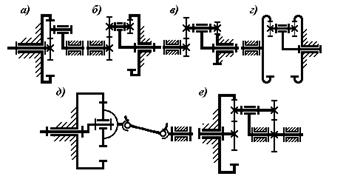
Рис. 5.26. Схемы планетарных механизмов

Механизм по схеме а получил название механизма Джеймса, а механизм по схеме в – механизм Давида. Наибольшее распространение получила схема а. Она характеризуется высоким к.п.д., практический диапазон передаточных отношений i=3 – 8. Механизмы по схемам в и г могут иметь очень большие передаточные отношения, но у них низкий к.п.д. По схеме е выполняются мотор – редукторы, представляющие в одном агрегате двигатель и редуктор. Особенно перспективна схема д, здесь всего два колеса, высокий к.п.д., большое передаточное отношение.

5.24. Аналитический метод определения передаточного отношения и угловых скоростей планетарных механизмов

Кинематический расчет планетарных механизмов значительно более сложен, чем рядовых механизмов. Он основан на методе обращения движения. Рассмотрим его на примере механизма на рис. 5.27. Считаем, что заданы числа зубьев колес Z₁, Z₂, Z₃, Z₄, угловая скорость входного колеса ω₁. Требуется определить передаточное отношение U_1н, угловую скорость выходного звена Н и угловую скорость колеса 2.

Сущность метода обращения движения состоит в следующем: придадим стойке механизма скорость вращения водила ω_н, но в противоположном направлении. Тогда водило окажется неподвижным в абсолютной системе отсчета, а остальные звенья приобретут дополнительную скорость – ω_н. Изобразим обращенный механизм рядом на схеме. Механизм с неподвижным водилом является зубчатым рядом, для него справедливы полученные ранее соотношения:

i₁₄^H = (ω₁ - ω_H) / (ω₄ – ω_H).

Здесь верхний индекс Н указывает, что параметры относятся к обращенному механизму. Согласно формуле (5.11) имеем:

U₁₄^H = - Z₂ Z₄ / Z₁ Z₃

Из формулы (5.12) после некоторых преобразований следует:

i_1H = ω₁ / ω_H = 1 - i₁₄^H .

Рис. 5.27. Планетарный и обращённый механизм

Полученная формула справедлива для любой схемы планетарного механизма. Она носит название формулы Виллиса.

Если требуется определить передаточное отношение от водила к колесу 1, то, имея в виду, что i_H1 = 1 / i_1H, получим

i_H1 = 1 / (1 - i₁₄^H).

Зная i_1H, можно найти ω_Н:

ω_Н = ω₁ / i_1H.

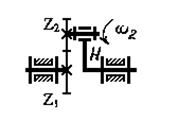
Рис. 5.28. Первая ступень планетарного механизма

Для определения скорости ω₂ следует рассмотреть одну ступень планетарного механизма и изобразить соответствующий ей обращенный механизм (рис.5.28). Для обращенного механизма

i₁₂ = (ω₁ – ω_H) / (ω₂ - ω_H).

Отсюда уже не представляет сложности определить ω₂.

5.25. Кинематический анализ автомобильного дифференциала

Рассмотренный метод кинематического исследования применим также к анализу дифференциальных зубчатых механизмов. Одним из наиболее известных является автомобильный дифференциал (рис.5.29). Его назначение – передача движения от карданного вала к колесам автомобиля. Механизм, представленный на рис.5.29, включает главную передачу, образованную коническими колесами Z₁и Z₂, корпус дифференциала, являющийся в то же время водилом дифференциального механизма, нескольких сателлитов Z₄ и двух центральных колес Z₃ и Z₅, жестко посаженных на полуоси колес.

Применим к этому механизму принцип обращения движения, сообщив

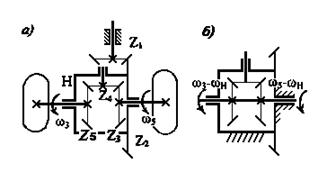
Рис. 5.29.Схема автомобильного дифференциала

ему скорость – ω_Н. На рис.5.29 представлен обращенный механизм. Для него можно записать

i₃₅^H = (ω₃ – ω_H) / (ω₅ – ω_H) = Z₅ / Z₃ .

Поскольку Z₅ = Z₃, i₃₅^H = -1. Знак минус указывает, что колеса Z₃ и Z₅ в обращенном механизме вращаются в противоположном направлении. Произведя подстановку, получим уравнение автомобильного дифференциала:

ω₃ + ω₅ = 2 ω_Н . (5.13)

Произведем анализ формулы (5.13). При движении по прямому участку дороги ω₃ = ω₅ = ω_Н, следовательно, дифференциал как бы жестко связывает полуоси, происходит кинематическая блокировка дифференциала. Совершенно по другому ведет себя дифференциал при движении по закруглению. Внешнее колесо движется с большой угловой скоростью, чем внутренне, но так, что их средняя скорость равна скорости водила.

Если бы колеса были связаны жесткой осью, происходило бы пробуксовка одного или обоих колес, ухудшая эксплуатацию автомобиля. В том случае, когда одно колесо свободно пробуксовывает, второе колесе неподвижно. Скорость буксующего колеса равно 2ω_Н. В таких случаях применят механическую блокировку дифференциала.

5.26. Замкнутые дифференциальные механизмы

Замкнутые дифференциальные механизмы позволяют получать огромные передаточные отношения при высоких к.п.д. Схемы таких механизмов чрезвычайно разнообразны. Рассмотрим механизм, построенный на основе трехколесного дифференциала (рис. 5.30). Для получения большого передаточного отношения необходимо, чтобы солнечные колеса Z₁ и Z₃ вращались в разные стороны. Это достигается тем, что вводится замыкающая кинематическая цепь, выполненная в виде рядового зубчатого механизма. В отдельных случаях возможно получение передаточного отношения порядка 700 -- 1000. При анализе таких механизмов их надо разделить на рядовую и планетарную ступени и проводить анализ каждой ступени, используя формулы, приведенные выше.

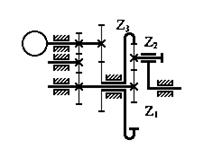
Рис. 5.30.Замкнутый дифференциал

5.27. Дифференциальные коробки передач

Дифференциальные коробки передач получили широкое распространение в транспортных машинах, например, тяжелых тракторах, лебедках и т.д. Они представляют дифференциальные механизмы, которые посредством фрикционных муфт можно преобразовать в различные комбинации рядовых и планетарных механизмов, при этом изменяется общее передаточное отношение механизма.

В качестве примера рассмотрим привод тяговой лебедки (рис. 5.31). Привод составлен на основе двух последовательно установленных трехколесных дифференциалов, снабженных ленточными тормозами Т₁ и Т₂ и фрикционными муфтами М₁ и М₂.

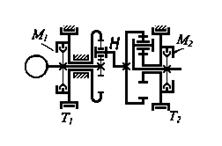
Рис. 5.31.Привод лебёдки

Здесь возможны четыре режима передач. При включении тормозов Т₁ и Т₂ дифференциалы работают как последовательно установленные планетарные механизмы, при этом обеспечивается наибольшее передаточное отношение. Для получения второй передачи включается тормоз Т₁ и муфта М₂. Тем самым блокируется второй дифференциал, который ведет себя как одно звено, работает только планетарный механизм первой ступени. Третья передача получается, если включить тормоз и муфту М₁. Четвертая передача получается при включении муфт М₁ и М₂. Это режим прямой передачи без редукции.

5.28. Графический метод анализа планетарных механизмов

В ряде случаев полезно произвести кинематическое исследование планетарного механизма графическим методом. В основе этого метода лежат два положения кинематики:

1. Скорость точки звена, совершающего вращательное движение, является линейной функцией радиуса вращения. В таком случае график зависимости скорости от радиуса есть прямая линия.

2. Любое плоское движение можно рассматривать как мгновенное вращательное движение вокруг МЦС (мгновенного центра скоростей).

В качестве примера рассмотрим механизм, представленный на рис. 5.32. Он включает планетарную и рядовую ступень, составленную колесами Z₅ и Z₆.

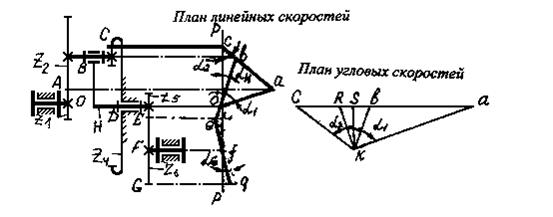
Рис. 5.32. Графический метод определения передаточного

Схема механизма должна быть построена в масштабе k_l = l_OA / OA. Справа от схемы построена линия полюсов р – р. От этой линии откладываются скорости точек звеньев в масштабе k_V = V_A / pa. Условимся положительные скорости направлять вправо, отрицательные – влево. Точки на линии полюсов находятся в проекционной связи с точками на механизме. Построение плана скоростей начинается с точки А. Скорость точки С равна нулю, эта точка является МЦС для блока сателлитов. Линия са на плане скоростей называется картиной распределения скоростей. Она обладает тем свойством, что на ней находятся концы векторов скоростей точек, лежащих на блоке сателлитов. Это свойство обосновано выше. Тогда, проведя линию проекционной связи, найдем скорость точки В. Соединив точки В и О, получим картину скоростей водила. Дальнейшее построение ясно из рисунка.

Покажем, что угловая скорость звена пропорциональна тангенсу угла наклона соответствующей картины скоростей. Это следует из соотношения:

ω₁ = V_A / L_OA = tg α k_ω. (5.14)

Аналогичные выражения можно записать для угловых скоростей остальных звеньев.

Формула (5.14) позволяет по углу наклона найти угловые скорости. Однако можно избегнуть необходимости этого расчета, если произвести дополнительное построение плана угловых скоростей. Выбирается произвольный вертикальный отрезок sk, из точки к строятся под углами α лучи до пересечения с горизонталью, проведенной через точку s. Из построений следует, что, например, tg α = sa / sk. Следовательно отрезки sa, sc, sb, se выражают в масштабе угловые скорости ω₁, ω₂, ω_Н, ω₆.

Графическое исследование дифференциального механизма производится аналогично, с той лишь разницей, что скорость точки С принимается равной нулю.

5.29. Условия соосности, соседства, сборки планетарных механизмов

В отличие от рядовых механизмов планетарный механизм может существовать только при выполнении определенных соотношений между числами зубьев колес.

Прежде всего должно быть выполнено условие соосности. Оно состоит в том, что оси центральных, солнечного и опорного, колес, а также водила должны совпадать. В противном случае механизм заклинит. Из рассмотрения схем на рис.5.33. следует:

а + b = c + d.

Поскольку колеса изображены их делительными окружностями, то нетрудно через диаметры делительных окружностей записанное выше равенство представить в виде:

Z₁ + Z₂ = Z₃ – Z₄.

Аналогичным образом для механизма по схеме б получено условие:

Z₁+ Z₂ = Z₄ – Z₃.

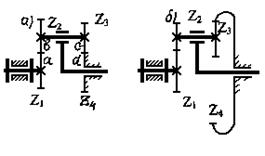
Рис. 5.33. Условие соосности

Условие соседства сателлитов выражается в том, что соседние сателлиты не должны касаться друг друга окружностями вершин (рис.5.34) Из геометрических построений соотношение:

2 r_2a < 2 R_H sin π / k,

где r_2a - радиус окружности вершин сателлита;

R_H – радиус водила;

k – число сателлитов в механизме.

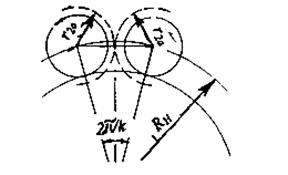
Рис. 5.34. Условие соседства

Выразив радиусы через модули и числа зубьев, и произведя преобразования, получим:

Sin π / k > (Z₂ + 2) / (Z₁ + Z₂). (5.15)

Формула (5.15) позволяет подсчитать максимальное число сателлитов. Впрочем, эту задачу можно решить и чисто графически.

При сборке трехколесного планетарного механизма может оказаться, что после установки первого сателлита остальные сателлиты установить нельзя. Это происходит потому, что поставленный первым сателлит полностью определяет взаимное положение центральных колес. Установим условия, налагаемые на числа зубьев, при которых будет происходить собираемость механизма (условие сборки) ,(рис. 5.35).

Будем считать, что сателлит имеет четное число зубьев, тогда впадины на центральных колесах можно расположить друг против друга. Повернем колесо 1 на целое число Е угловых шагов φ₁^Е = Е φ₁, где φ₁ = 2π/Z₁.Тогда впадины между зубьями расположатся друг против друга и можно поставить следующий сателлит. Подсчитаем угол поворота водила:

φ₁^Е / φ_H^E = i_1H,

отсюда

φ_H ^E = 2π E / Z₁ i_1H.

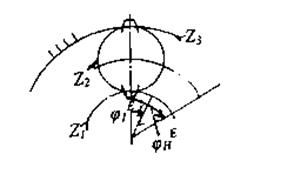
Рис. 5.35. Условие сборки

Воспользовавшись формулой Виллиса, выразим i_1H через U₁₃^H и преобразуем вышезаписанную формулу:

φ_H^E = 2π E / (Z₁ + Z₃).

Таким образом можно установить к сателлитов, если расположить их равномерно:

к = 2π/ φ_H^E = (Z₁ + Z₃) / E.

Поскольку к – целое число, Z₁ + Z₃ должно быть кратно числу сателлитов. Аналогичные результаты получены и при нечетном числе зубьев сателлитов. Для передач с двойными сателлитами условие сборки можно получить аналогичным образом.

5.30. Пример синтеза планетарного механизма

Рассмотрим методику синтеза планетарного механизма, ограничиваясь соблюдением условия заданного передаточного отношения и условия соосности. Пусть выбрана схема механизма (рис.5.36), для которой надо подобрать числа зубьев, обеспечивающие передаточное отношение, например, равное 12.

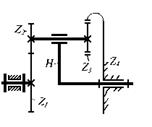
Рис. 5.36. Схема планетарного механизма

1. Определяем передаточное отношение соответствующего обращенного механизма:

i₁₄^H =1 – i_1H = - 11.

2.Разложим полученное передаточное отношение на множители. Здесь возможны разнообразные варианты, например:

i₁₄^H = Z₂ Z₄ / Z₁ Z₃ = 220 / 20 =4 ▪ 55 / 4 ▪ 5.

3.Запишем условие соосности и проверим его выполнение для принятых чисел зубьев:

Z₁ + Z₂ = 4 + 4 = 8,

Z₄ – Z₃ = 55 – 5 = 50.

4.Условие соосности, как правило, не выполняется. Для его выполнения нужно умножить верхнюю формулу на 50, а нижнюю – на 8. Тогда

Z₁ = 200 , Z₂ = 200, Z₄ = 440, Z₃ = 40.

Полученные числа зубьев можно сократить так, чтобы получились реально выполнимые колеса с числом зубьев в пределах 10 – 100.

5.31. Волновая передача

В 1959 году Массер (США) запатентовал зубчатую передачу, которая в настоящее время пользуется большой популярностью. Ее основные достоинства – большое передаточное отношение, высокий к.п.д., способность передавать движение в герметичные полости, многопарность зацепления (до 30% зубьев), малое скольжение и износ.

В волновой передаче одно из колес выполняется гибким, способным деформироваться под действием звена, называемого генератором волн. Волновые передачи весьма разнообразны. Чаще всего они выполняются с неподвижным жестким звеном и внутренним гибким колесом. Возможны двухволновые и многоволновые механизмы с генератором в виде эллипсовидного звена с шариковым подшипником . Преобразование движения происходит за счет деформации упругой оболочки.

Легче всего принцип действия волновой передачи объяснить, исходя из аналогии с планетарной передачей. Волновая передача, представленная на рис. 5.37,а эквивалентна двухколесной планетарной передаче (рис. 5.37, б), у которой число зубьев сателлита равно числу зубьев гибкого колеса.

Для планетарного механизма

i₁₂^H = (ω₁ – ω_H) / (ω₂ – ω_H) = Z₂ / Z₁;

ω₁ / ω_H = 1 – Z₂ / Z₁;

i_пл = ω_H / ω₁ = 1 / (1 – Z₂ / Z₁).

Если Z₂ / Z₁ ≈ 1, то i_пл получается очень большим и имеет отрицательный знак.

Еще один вариант исполнения волновой передачи представлен на рис. 5.37 в. Здесь посредством гибкой стенки герметично разъединены полости А и Б Планетарным аналогом служит механизм с поступательно движущимся сателлитом. Для него

i₁₂^H = (ω₁ – ω_H) / (ω₂ – ω_H) = Z₂ / Z₁;

i_2H = ω₂ / ω₁ = 1 – i₂₁^H ;

i_пл = ω_H / ω₂ = (Z₂ / Z₁) / (Z₂/ Z₁ – 1).

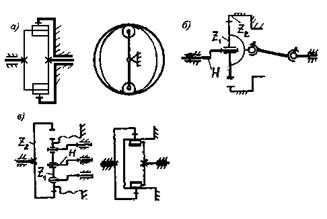
Рис. 5.37. Волновые передачи

Здесь передаточное отношение положительно, что обусловливает большой к.п.д. Одним из достоинств волновой передачи является высокий к.п.д. Это обусловливает его применение в тех случаях, когда экономия энергии чрезвычайно необходима, например, в космической технике.

5.32. Планетарные механизмы робототехнического назначения

Планетарные механизмы находят широкое применение в различных робототехнических устройствах. В некоторых случаях они обеспечивают основные движения роботов, как например механизм ориентации кисти робота. В основе его использован зубчатый дифференциальный механизм с коническими колесами.

Для объяснения принципа работы этих достаточно своеобразных механизмов рассмотрим вначале схему простейшего конического дифференциала (рис. 5.38,а).

Угловая скорость колеса 2 находится из соотношения

,

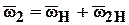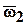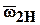где и – векторы абсолютной угловой скорости соответствен­но для колеса 2 и водила Н; 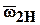– вектор угловой скорости звена 2 отно­сительно водила.

Сообщим обращенное движение всему механизму вокруг колеса 1 со скоростью водила, но в противоположном направлении. Это очевидно не изменит относительного движения звеньев, однако позволит рассматри­вать обращенный механизм как рядовую коническую передачу (рис. 5.38,6).

Для нее справедливо выражение

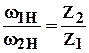, (5.16)

где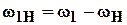

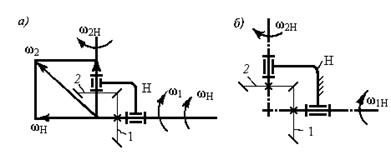
Рис. 5.38. Двухколесный конический дифференциал ( а ) и

его обра­щенная схема ( б ).

Анализ формулы ( 5.16 ) показывает, что при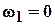

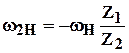– механизм планетарный;

при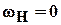

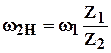– механизм рядовой.

Конический дифференциал применяется в кисти робота. Из приве­денных выше соотношений вытекает, что при качании кисти имеет место и ее ротация, т. е. поворот вокруг собственной оси. Чтобы разделить эти

движения, следует сообщить центральному колесу 1 угловую скорость .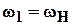

Уравнение кинематической связи для симметричного конического дифференциала ( рис. 5.39 ), также широко применяемого в роботах, име­ет вид

.

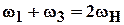Из него следует, что если скорости центральных колес одинаковы, дифференциал заблокирован 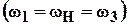, а если одно из центральных колес неподвижно, 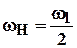, т.е. скорость водила равна половине ско­рости ведущего колеса при том же направлении вращения.

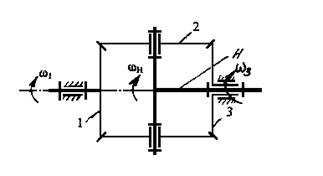
Рис. 5.39. Симметричный конический дифференциал

Для преобразования вращательного движения в поступательное применяется реечная зубчатая передача, представляющая по существу ва­риант зубчатой передачи, у которой зубчатое колесо имеет бесконечно большой радиус.

Реечные передачи могут выполняться и по дифференциальным схе­мам

Линейные скорости точек механизма ( рис. 5.40) связаны соотношением V_A=V_H+V_AH, ( 5.17)

где V_H – скорость водила; V_AH – скорость точки А относительно во­дила.

Сообщим механизму обращенное поступательное движение со ско­ростью – V_H. Для обращенного механизма

V_AH=V_A-V_H=-(V_B–V_H). (5.18)

После подстановки выражения (5.18) в (5.17) получим уравнение реечного дифференциала

V_A=2V_H -V_B.

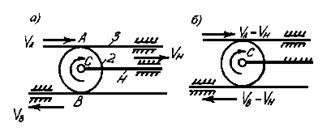
Рис. 5.40. Реечный дифференциал ( а ) и его обращённая схема ( б )

Если скорость точки В равна нулю, то V_A = 2Vh , т.е. происходит удвоение скорости водила, а значит ход звена 3 в два раза больше хода водила.

В роботах находит применение планетарный механизм с гибким тяговым органом, в качестве которого может служить цепь. Цепь охватыва­ет неподвижную звездочку 1 и подвижную звездочку 2, закрепленную на несущем подвижном звене (рис. 5.41,а).

Звездочка 2 здесь играет роль сателлита, а несущее подвижное звено – роль водила. При вращении водила с угловой скоростью 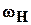сателлит из-за наличия гибкой связи приобретает абсолютную угловую скорость 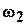направлении противоположном вращению водила.

Применим принцип обращения движения и рассмотрим образовав­шийся механизм (рис. 5. 41,б). Это рядовая цепная передача, для которой кинематическое уравнение имеет вид

,

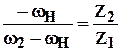откуда следует уравнение для планетарного механизма:

.

Пусть, например, 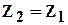,тогда 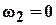и звездочка 2 при движении водила сохраняет ориентацию неизменной. Если же 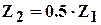, то .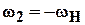

Рис. 5.41. Цепной планетарный механизм

Оба механизма используются в манипуляторах: первый – для развяз­ки вращательных движений; второй – для получения прямолинейного движения за счет использования двух звеньев равной длины, вращающих­ся с одинаковыми скоростями, но в противоположных направлениях.

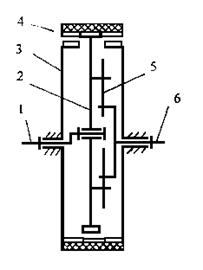
Рнс.5.42.Зубчато-ременный планетарный редуктор: 1– входной вал,

2 – подвижный шкив, 3 – неподвижный шкив-звездочка, 4 – зубчатый ре­мень, 5 – крестовая муфта, 6 – выходной вал.

На основе описанного выше цепного планетарного механизма авто­ром этого пособия разработан зубчато-ременный планетарный редуктор. Кинематика этого редуктора полностью описывается приведенными выше формулами. Его достоинства – малые габариты при больших передаточ­ных отношениях благодаря тому, что разность чисел зубьев зубчатых шки­вов 2 и 3 равна единице. Кроме того, из-за использования зубчатого ремня уменьшен шум передачи и уменьшена масса по сравнению с плане­тарными механизмами обычного типа.

Из-за наличия большого числа зубьев, находящихся в зацеплении, повышается нагрузочная способность передачи. Благодаря использованию в передаче ремня уменьшается момент инерции подвижных частей, а значит улучшаются динамические характеристики привода. Ремень изготавливается из резины или полиуретана. Ременная передача может работать в условиях отсутствия смазки.

К