Сложная цепь с магнитносвязанными катушками

В сложной цепи магнитосвязанные катушки могут находиться в любых ветвях. Так как направления токов в ветвях схемы выбираются произвольно, то токи в ветвях, содержа­щих магнитносвязанные катушки, могут быть направ­лены как согласно, так и встречно.

Расчет токов в сложной схеме с магнитносвязанными катушками произ­водится, как правило, методом законов Кирхгофа. К расчету таких цепей не­применим метод узловых по­тенциалов и метод эквивалентного генератора. Учет всех слагаемых в уравнениях метода контурных токов довольно сложен, по этой причине его также не применяют.

Рассмотрим расчет схемы на конкретном примере рис. 73:

Система уравнений Кирхгофа:

		(1)   (2)   (3)

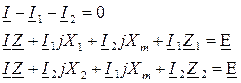
При составлении уравнений по второму закону Кирхгофа следует соблю­дать правило полярности токов, а именно, падение напряжения от собственного тока ветви на собственном реактивном сопротивлении (I₁jX₁) и падение напря­жения на взаимном реактивном сопротив­лении от тока связанной ветви (I₂jX_М) принимаются одного знака при согласном направлении этих токов, и противо­положного знака при встречном направлении (в рассматриваемом при­мере токи направлены согласно).

Сделаем подстановки в уравнение (2) I₂ = I - I₁ и в уравнение (3) I₁ = I - I₂, в результате получим новую систему уравнений:

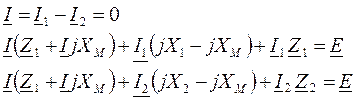
Новой системе уравнений соответствует некоторая новая эквивалентная схема без магнитных связей (рис. 74):

Если ветви с магнитносвязанными катушкам присоединены к общему узлу одноимен­ными выводами, то магнитная развязка имеет вид рис. 75:

Если ветви с магнитносвязанными катушкам присоединены к общему узлу разно­именными выводами, то магнитная развязка имеет вид рис. 76:

Замена исходной схемы с магнитносвязанными катушками эквивалент­ной схемой без магнитных связей называется развязкой магнитных связей или магнитной развязкой. Маг­нитная развязка электрических схем применяется для упрощения их расчета. После выполне­ния магнитной развязки к расчету схемы применим любой метод расчета сложных схем.