Круговая диаграмма для произвольного тока и напряжения в сложной цепи

Пусть в схеме сложной цепи изменяется параметр сопротивления в к-той ветви Z_к=Z_кe^jjк так, что фазный угол j_к= const, а модуль Z_к=0÷¥ = var – пере­менный параметр.

Выделим к-тую ветвь из сложной схемы, а остальную часть схемы по от­ношению к ветви заменим эквивалентным генератором напряжения с парамет­рами E_э = U_хх, Z₀= Z₀e^jjo = Z_вх (рис 82):

Таким образом, получившаяся эквивалентная схема рис. 82 ничем не от­ли­чается от рассмотренной ранее схемы рис. 81, и, следовательно, для пере­менных векторов I_к, U_к по аналогии могут быть могут быть записанные уравне­ния дуги в комплексной форме, напри­мер:

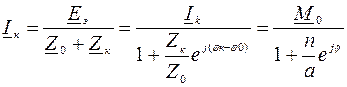- есть уравнение дуги.

Докажем, что для тока I_n произвольной n- ой ветви сложной схемы также может быть получено уравнение дуги в комплексной форме.

В соответствии с теоремой о линейных отношениях исследуемый I_n и ток I_к связаны между собой линейной зависимостью:

I_n = A + B∙I_к,

где А, В – комплексные коэффициенты, значения которых можно найти из крайних режимов схемы (холостого хода и короткого замыкания).

В режиме холостого хода Z_к = ¥, I_кхх = 0, тогда I_nxx= A.

В режиме короткого замыкания Z_к = 0, тогда I_nкз = A + B∙I_ккз = I_nxx + B∙I_ккз , откуда получаем:

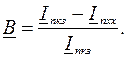
Подставим найденные значения коэффициентов А и В и уравнение дуги для тока I_к в уравнение связи:

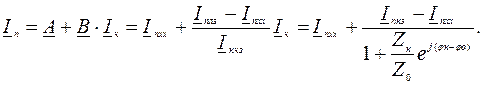
Уравнение для произвольного тока I_n состоит из суммы двух векторов: а) постоянного вектора I_nxx, равного его значению в режиме холостого хода при Z_к = ¥, и б) переменного вектора, изменяющегося по дуге окружности с хордой I_nкз- I_nxx. При построе­нии круговой диаграммы тока I_n по этому уравнению вна­чале строится его постоянная со­ставляющая I_nxx, в конце которой строится кру­говая диаграмма для переменной составляющей, результирующий вектор полу­чают как сумму двух составляющих.

Уравнение круговой диаграммы для произвольного напряжения может быть получено путем аналогичных логических выводов.