Теоретические основы комплексного метода расчета цепей

Переменного тока

Из курса математики известно, что комплексное число Z может быть представлено в следующих трех формах: показательной, тригонометрической и алгебраической:

показательная тригонометрическая алгебраическая

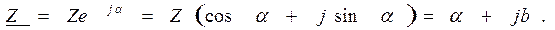
В основе перехода от одной формы комплексного числа к другой лежит известная из математики формула Эйлера :

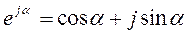
Здесь обозначены:

j = 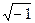– мнимое единичное число,

Z – модуль комплексного числа,

a - аргумент комплексного числа,

а – вещественная часть комплексного числа,

jb – мнимая часть комплексного числа.

Соотношения между коэффициентами различных форм комплексного числа выте­кают из формулы Эйлера :

a = Z cosa ; b = Z sina ; Z = 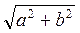; a = arctg .

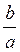Приведем наиболее часто встречающиеся численные соотношения :

e^j0 = 1 ; e^{± j180°} = -1 ; e ^j90° = +j ; e^-j90° = -j ;

1/j = -j ; j² = -1 ; j³ = -j ; и т.д.

Комплексное число Z = Z e^ja = a + jb может быть изображено векто­ром на ком­плексной плоскости (рис. 38), при этом алгебраической форме числа 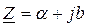соответствует декартовая система координат (a ® x; b ® y), а показа­тельной форме числа Z = - по­лярная система координат (Z ® r; a ® q).

Можно утверждать, что каждой точке (вектору) на комплексной плоско­сти соответ­ствует определенное комплексное число, и наоборот, каждому ком­плексному числу соответ­ствует определенная точка (вектор) на комплексной плоскости.

Известно, что синусоидальную функцию можно изобразить вектором, а вектор в свою очередь можно представить комплексным числом. Таким обра­зом, синусоидальные токи и напряжения, характеризующие установившийся режим цепи переменного тока, могут быть представлены комплексными чис­лами :

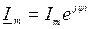Û - комплексная амплитуда,

Û 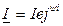- комплексное действующее значение. Здесь Û -знак соответствия.

При расчете цепей переменного тока возникает необходимость выпол­нения различ­ного рода математических операций с синусоидальными функ­циями. При замене синусои­дальных функций (оригиналов) комплексными чис­лами (изображениями) соответствующие математические операции выполня­ются с комплексными числами.

Сложение (вычитание) комплексных чисел производится в алгебраиче­ской форме

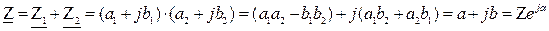
Умножение комплексных чисел может выполняться, как в алгебраиче­ской, так и в показательной формах:

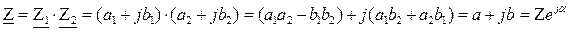
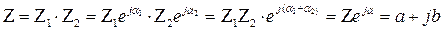
Деление комплексных чисел может выполняться как в алгебраической, так и в пока­зательной формах:

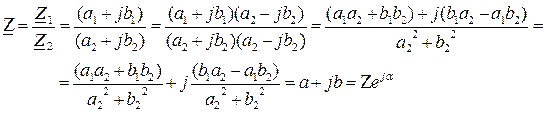
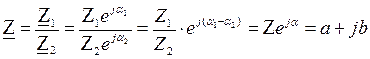
Возведение в степень (извлечение корня) комплексного числа выполня­ется только в показательной форме:

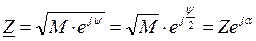
Установим порядок дифференцирования и интегрирования синусои­дальных функций в комплексной форме. Пусть задана некоторая функция тока и ее комплексное изображение:

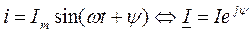
Производная и интеграл от этой функции их комплексные изображения будут равны:

;

.

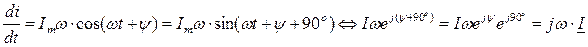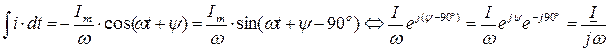Таким образом, дифференцированию синусоидальной функции времени соответст­вует в комплексной форме умножение ее комплексного изображения на множитель jw, а ин­тегрированию – соответственно деление на тот же коэф­фициент:

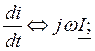
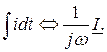
Замена математических операций 2-го рода (дифференцирование, интег­рирование) операциями 1-го рода (умножение, деление) существенно упрощает расчет цепей перемен­ного тока в комплексной форме.

Современные инженерные калькуляторы в режиме «compl» позволяют выполнять все действия с комплексными числами непосредственно так же, как с обычными числами. При этом следует принять во внимание, что калькулятор выполняет действия над комплекс­ными числами только в алгебраической форме 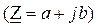и результаты расчета выдает также в алгебраической форме. Если исходные комплексные числа заданы в показательной форме 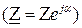, то после их ввода необходимо выполнить операцию преобразования их в алгеб­раическую форму.

Комплексный метод расчета цепей переменного тока был разработан в 1910-1912гг. американским инженером Штейнметцом и сыграл большую роль в развитии теории электри­ческих цепей переменного тока.