Взаимодействие электромагнитных волн с плазмой

4.4.1. Отражение волн от границы плазмы.

Рассмотрим падение электромагнитной волны на границу плазмы. Будем считать границу плазмы резкой и плоской. Ситуация представлена на рисунке 4.4.1

Рисунок 4.4.1. Падение электромагнитной волны на границу холодной плазмы.

Падающая волна: 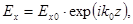(4.4.1.1)

Отраженная волна: 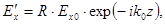(4.4.1.2)

Прошедшая волна: 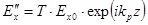. (4.4.1.3)

Здесь R – коэффициент отражения, T – коэффициент прохождения, 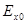- амплитуда падающей волны. Дисперсионные соотношения для вакуумной области и для области, занятой плазмой выглядят соответственно:

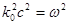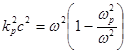и . (4.4.1.4)

Необходимым и достаточным условием непрерывности электромагнитного поля на незаряженной границе без тока является условие непрерывности тангенциальных компонент векторов поля

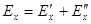
Из этого условия определяются коэффициенты отражения и прохождения для плоской границы однородной изотропной холодной плазмы:

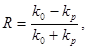
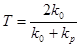. (4.4.1.5)

Выражения (4.4.1.5) получены с учетом того, что, положив z=0, мы имеем из (4.4.1.1) - (4.4.1.3)

,

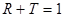а в ближайшей окрестности можем воспользоваться разложением экспонент в ряд Тейлора, ограничиваясь первым, линейным, членом разложения.

Для волн, частота которых много больше плазменной, 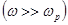, из (4.4.1.4) следует, что 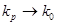и коэффициент отражения близок к 0, а коэффициент прохождения – к 1. При 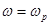, 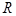становится равным 1, а Т=0, т.е. плазма отражает падающую волну полностью.

4.4.2. Глубина высокочастотного скин-слоя.

Если частота падающей волны много меньше плазменной частоты,

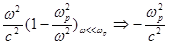, (4.4.2.1)

то волновое число становится мнимым

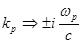(4.4.2.2)

и электрическое поле спадает экспоненциально в направлении от границы внутрь плазмы:

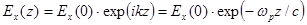(4.4.2.3)

т.е. волна быстро затухает в этом направлении. Расстояние, на котором поле уменьшается в е раз называется глубиной плазменного скин–слоя:

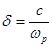(4.4.2.3)

4.4.3. Сила высокочастотного давления.

Рассмотрим движение электрона в осциллирующих полях 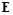и ,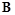

связанных с электромагнитной волной. Постоянными полям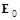и и 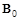пренебрегаем. Уравнение движения электрона имеет вид:

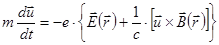(4.4.3.1)

Пусть

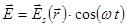(4.4.3.2)

где 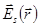- пространственное распределение поля. Член 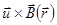второго порядка малости и источник нелинейности.

В первом приближении им можно пренебречь. Можно также считать, что 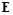равно значению в точке 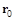(начальное положение частицы)

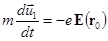(4.4.3.3)

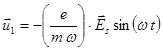(4.4.3.4)

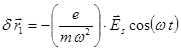(5.2.5)

Анализируя величины второго порядка, нужно разложить 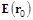в ряд вблизи :

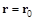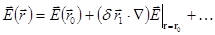(4.4.3.6)

В уравнении движения теперь придется учесть член 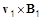, где 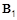определяется из уравнения Максвелла :

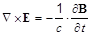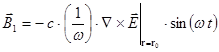(4.4.3.7)

Часть уравнения (4.4.3.1), имеющую второй порядок малости, можно записать:

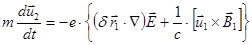(4.4.3.8)

Подставляя сюда 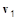и 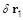из (4.4.3.4) и (4.4.3.5) и усредняя по времени, имеем:

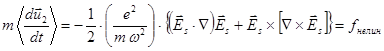(4.4.3.9)

здесь использовано то, что .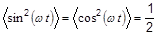

Раскрываем двойное векторное произведение

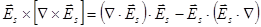
и имеем из (4.4.3.9):

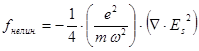(4.4.3.10)

Это эффективное значение силы, действующей на отдельный электрон. Чтобы получить силу, действующую на 1см³, нужно умножить на плотность электронов 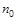, которую можно выразить через 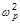. Используя соотношение 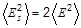, имеем для силы высокочастотного давления:

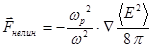(4.4.3.11)