Приложение 2. Задачи

Глава 1

1.1.Вычислить величины дебаевского радиуса и плазменной частоты для следующих случаев :

А) плазма токамака ( n = 10¹⁴ см^-3 , Т_е = 40 КэВ );

Б) разряд в ионном источнике ( n = 10¹² см^-3 , Т_е = 8 эВ );

В) ионосфера Земли ( n = 10⁶ см^-3 , Т_е = 0.1 эВ ).

1.2.Вычислить число частиц в дебаевской сфере для тех же случаев.

1.3.Вычислить давление плазмы в термоядерном реакторе ( n = 5. 10¹⁴ см^-3 , Т_е = 30 КэВ ).

1.4.Температура плазмы в установке Токамак равна 20кэВ. Скольким

градусам Кельвина это соответствует?

1.4.Вычислить плотность тепловой энергии плазмы в термоядерной

установке, если ее плотность 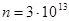см^-3, а температура 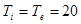кэВ.

1.5.Оценить плотность кулоновской энергии для термоядерной плазмы по параметрам предыдущей задачи.

1.6.Вычислить степень ионизации для малой примеси и для основной

компоненты плазмы, если константа равновесия ионизации задана.

Решение:

Степень ионизации 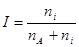. Концентрация электронов определяется основной компонентой плазмы, поэтому для примеси ее можно считать заданной. Тогда, имея в виду заданную константу равновесия ионизации.

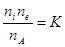, получаем . ( ; )

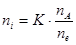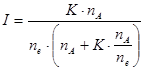Для основной компоненты концентрация электронов определяется равновесием ионизации. При однократной ионизации 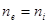. Тогда из соотношения равновесия следует 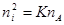. Если степень ионизации велика, то следует исходить из заданности начальной концентрации атомов 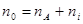. Тогда 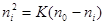или . Взяв положительный корень этого квадратного уравнения, получаем выражение для степени ионизации:

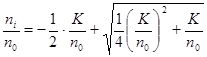
Если степень ионизации мала, то 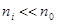и 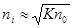, откуда .

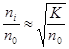1.7. Найти температурную зависимость равновесной концентрации электронов для слабоионизованной плазмы, имеющей потенциал ионизации основной компоненты J.

Решение:

Из результата предыдущей задачи следует, что для слабоионизованной плазмы 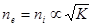. По формуле Саха видно, что константа равновесия зависит от температуры следующим образом

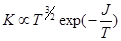
При малой степени ионизации можно пренебречь статистическими весами возбужденных состояний и учитывать только статвеса основных состояний (которые от температуры не зависят). При этом

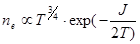
1.8.Найти зависимость степени ионизации от концентрации для стационарного (но не равновесного) состояния в плазме, из которой излучение выходит свободно, так, что ионизация производится электронным ударом, а рекомбинация – с излучением. Ионизацией под действием излучения можно пренебречь из-за прозрачности плазмы, тройной рекомбинацией – из-за малой плотности.

Решение:

Приравнивая скорости ионизации электронами и рекомбинации парными столкновениями с излучением: 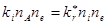, имеем:

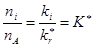. Величина 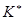здесь уже не может быть найдена из термодинамики. Она определится сечениями процессов ионизации и рекомбинации. Стационарное состояние ионизации не зависит от концентрации электронов. Степень ионизации выразится соотношением:

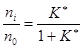, в которое не входит концентрация электронов. Это не зависит от того, является ли вещество малой примесью или это основная компонента плазмы.

Глава 2

2.1.Вычислить ларморовский радиус

А) дейтона с энергией 15 КэВ, движущегося в однородноммагнитном поле 0.85 Т под углом 60⁰ к силовым линиям;

Б) электрона с энергией 10 КэВ движущегося в однородном магнитном поле 0.6 Т под углом 45⁰ к силовым линиям;

В) ядра атома гелия с энергией 3 МэВ движущегося в однородном магнитном поле 0.7 Т под углом 45⁰ к силовым линиям.

2.2. Вычислить значения циклотронных частот для тех же случаев.

2.3.Вычислить скорость дрейфа электрона в скрещенных электрическом ( E = 100 В/см) и

магнитном H = 0.1 T ) полях.

2.4.Рассмотреть движение заряженной частицы в поле прямого тока.

2.5.Выразить в явном виде условие применимости дрейфового приближения для движения заряженной частицы в магнитном поле прямого тока.

2.6.Плазменный цилиндр находится в скрещенных полях: продольном

магнитном и радиальном электрическом. Найти энергию системы, считая, что вращение плазмы происходит со скоростью электрического дрейфа.

2.7.Сравнивая энергию системы по задаче 2.6. с энергией цилиндрического конденсатора, определить эффективную диэлектрическую проницаемость плазмы.

2.8.Плазма, цилиндрической формы, имеет диаметр D и находится во внешнем продольном магнитном поле. Сформулировать количественно условие ее замагниченности.

Решение:

Чтобы частицы плазмы не уходили сразу на стенку установки, их ларморовский радиус должен быть существенно меньше характерного поперечногоразмера системы (в данном случае – диаметра установки. Таким образом имеем условие:

,

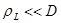кторое, после подстановки выражения для ларморовского радиуса, запишется (с точностью до множителя, порядка единицы):

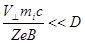
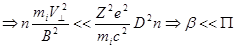
Где 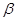- отношение газокинетического давления плазмы (плотность тепловой энергии) к магнитному; - погонное число частиц 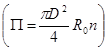, R₀= 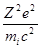- так называемый классический радиус частицы, определяемый из условия равенства кулоновской энергии частицы и ее собственной энергии .

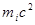2.9.Как изменится уравнение диффузии магнитного поля в плазму, если учесть токи смещения?

Решение:

Выпишем нужное нам уравнение Максвелла с учетом тока смещения: 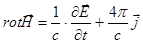, выразим из него 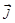и подставим в (2.2.27). Получим:

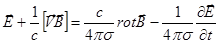. Взяв ротор от обеих частей равенства, и учитывая, что 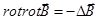, получим уточненное уравнение диффузии магнитного поля:

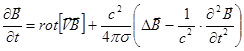вместо прежнего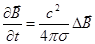

2.10. Плазма, находящаяся в зеркальной ловушке с пробочным отношением R_m = 4, имеет изотропное распределение частиц по скоростям. Столкновения отсутствуют, так что частицы, попавшие в конус потерь, сразу уходят, а не попавшие – остаются. Определить долю захваченных частиц.

Указание:

Покидают систему частицы, у которых в центральной части ловушки питч-угол орбиты меньше значения, определяемого соотношением:

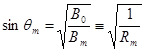. В интересующем нас случае R_m=4, следовательно, в ловушке останутся частицы с питч-углами, синус которых превышает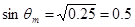

Глава 3

3.1. В установке получен высокий вакуум при давлении остаточного газа (азот) 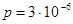Тор. Перевести это значение в Па. Вычислить длину свободного пробега молекул газа.

3.2.Пучок электронов с энергией 80 эВ проходит через молекулярный

водород. Определить число протонов, рождающихся в секунду в 1 см³ .

3.3.Водород, десорбируемый со стенки плазменной установки в виде

молекул, летит в плазму со следующими параметрами 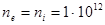см^-3 , 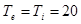эВ. Определить глубину проникновения его в плазму в виде нейтрального газа.

3.4.Решить предыдущую задачу для параметров термоядерной плазмы по

задаче 2.2.

3.5.Вычислить значение кулоновского логарифма для газоразрядной плазмы

плотностью 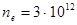см^-3 при температуре электроно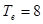в эВ.

3.6.Пучок электронов с энергией 40 эВ влетает в газоразрядную водородную

плазму с параметрами, данными в предыдущей задаче. Определить характерное время его торможения за счет кулоновских столкновений.

3.7.Пучок быстрых атомов водорода, инжектированный тангенциально в

плазму токамака, захватывается в ней в виде быстрых ионов, движущихся вдоль оси установки. Оценить количество оборотов, которое ионы пучка совершат до потери своей энергии (до уровня температуры плазмы), если энергия инжекции равна 1МэВ, а параметры плазмы: 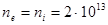см^-3 , 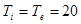кэВ, при большом радиусе токамака R= 5.5 м.

Глава 4

4.1.Для определения плотности плазмы используется СВЧ интерферометр с длиной волны 6 мм. До какого значения плотности эти измерения могут производиться.

4.2.Вывести дисперсионное соотношение для высокочастотных электромагнитных волн, распространяющихся в холодной плазме без магнитного поля. Столкновениями пренебречь.

4.3.Связь с космическим кораблем поддерживается с помощью передатчика, работающего на частоте 450 МГц. Достаточна ли высока частота для прохождения ионосферы ? Какова критическая плотность плазмы, вызывающая прерывание связи ?

4.4.Каково должно быть соотношение между циклотронными частотами и плазменной частотой чтобы альфвеновская скорость была много меньше скорости света?

4.5.Вычислить групповую скорость прямых магнитозвуковых волн в плотной плазме.

4.6.Выразить фазовую скорость волн на электронной плазменной частоте в

функции плотности и температуры плазмы.

4.8. Выразить фазовую скорость магнитозвуковой волны как функцию частоты в плотной горячей плазме.

Глава 5

5.1.Плотность ионного тока насыщения, приходящего на плоский зонд 10

мА\см² . Вычислить плотность плазмы, если температура электронов равна 5 эВ.

5.2.Источник пучка ионов водорода (протия) , используемый в инжекторе

быстрых атомов токамака Т-15, формирует пучок с энергией 40 КэВ. Считая, что ионно-оптическая система (ИОС) источника может быть представлена как эффективный плоский диод, оценить плотность тока, при которой он работает . Учесть при этом, что напряжение между электродами ИОС ограничено условием пробоя U[KВ] = 80 ( l [см] )^1/2 .

5.3. Критерий существования стабильного слоя выведен для случая плазмы с холодными ионами. Как изменится пороговая величина средней скорости ионного потока при наличии теплового размытия ионных скоростей?

Ответ:

Пороговая скорость должна быть больше значения, полученного для холодных ионов. Важна величина объемного заряда, создаваемого ионной компонентой, а, следовательно – пролетной плотности ионов. Ионы, имеющие скорости большие средней, дают меньший вклад в пролетную плотность, чем относительно медленные ионы. Разброс в сторону меньших скоростей сильнее увеличивает пролетную плотность, чем уменьшает ее разброс в сторону больших скоростей. Это должно быть скомпенсировано большей средней скоростью.