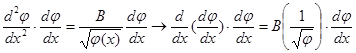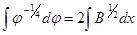Волновые методы исследования плазмы

4.5.1. Измерение плотности плазмы по отсечке СВЧ излучения

Полное отражение электромагнитной волны от плазмы при равенстве частоты этой волны плазменной частоте используется для определения плотности плазмы. Применяемая при этом схема измерения приведена на рисунке 4.5.1.

Рисунок 4.5.1. Схема измерения плотности плазмы по отсечке СВЧ излучения.

Определяется частота, при которой интенсивность проходящего на приемник сигнала обращается в нуль. Значение плотности вычисляется из условия отсечки

.

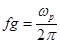
При этом

.

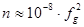Существенным недостатком описанной схемы является то, что отсечка происходит, если плотность плазмы превышает критическую даже локально в любом месте на пути волнового луча. Плазма может быть сосредоточена, к примеру, в малой центральной области и практически отсутствовать во всем объеме установки.

4.5.2. СВЧ интерферометрия

Гораздо более информативна методика СВЧ интерферометра. Плотность плазмы измеряется при этом по сдвигу фазы электромагнитной волны при ее прохождении сквозь плазму. Схема измерения видоизменяется (см. рисунок 4.5.2). Часть сигнала, выходящего из генератора, ответвляется в так называемый опорный канал, в котором установлены аттенюфтор и фазовращатель, позволяющие регулировать амплитуду и фазу волны в опорном сигнале. Опорный сигнал затем складывается с сигналом, прошедшим через плазму по основному измерительному каналу. Регулировка опорного сигнала производится так, чтобы в отсутствие плазмы сигнал на регистраторе был равен нулю, т.е. чтобы происходило взаимное погашение волн (Фазы сдвинуты на 180⁰). При появлении плазмы в измерительном канале, фаза проходящей по нему волны сдвигается и измеритель регистрирует появление сигнала.

Фазовый сдвиг, возникающий при прохождении электромагнитной волны сквозь плазму, легко рассчитывается из следующих соображений. Сдвиг фазы измерительной и опорной волн определяется различием фазовых скоростей в опорном плече (вакуумная скорость, с) и в измерительном плече (скорость распространения волны в плазме 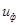). При одинаковом геометрическом расстоянии l времена прохождения точки с одинаковой фазой опорного и измерительного плеча

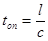и ,

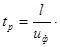Разность их 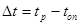и определит фазовый сдвиг :

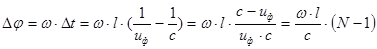(4.5.2.1)

Рисунок 4.5.2. Схема СВЧ интерферометра.

Показатель преломления 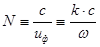электромагнитной волны, распространяющейся в холодной плазме дается выражением: 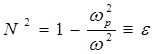, с помощью которого получаем

,

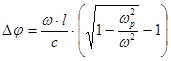или, считая, что 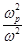<<1, и используя разложение по малому параметру

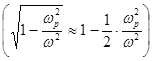, получаем 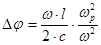. (4.5.2.2)

Используя выражение для плазменной частоты : 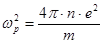и имея в виду, что частота, на которой производится измерения, определяет критическое значение плотности плазмы, получим окончательно

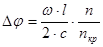(4.5.2.3)

Глава 5. Объемный заряд в плазме

5.1. Задача о плоском диоде

Начнем с рассмотрения модели, которую можно представить как предельный

случай пристеночного слоя плазмы. Рассмотрим плоский диод – систему, состоящую из двух бесконечных пластин 1 и 2, расположенных параллельно одна другой на расстоянии d. Одна из пластин является эмиттером заряженных частиц, ускоряемых по направлению ко второй разностью потенциалов U =  - _1. Без ограничения общности можем считать потенциал эмиттера нулевым (₁ = 0). Пусть ось x направлена перпендикулярно пластинам, плотность тока частиц, эмиттируемых с нулевыми начальными скоростями пластиной 1 равна j , масса каждой частицы m , а ее заряд q . Будем искать распределение потенциала между пластинами вдоль оси x .

Воспользуемся уравнением Пуассона, которое в данном случае будет одномерным

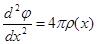(5.1)

где (x) en(x)- распределение плотности заряда вдоль оси x . С учетом сохранения плотности тока вдоль x : j = en(x) u(x) = const. (u – скорость частиц вдоль оси, зависящая от пройденной разности потенциалов и, следовательно, от координаты) выразим (x):

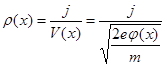(5.2)

и, подставив в (5.1), получим

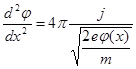(5.3)

Обозначив: 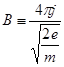, перепишем уравнение (5.1.3) в виде:

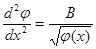(5.3а)

Первый интеграл уравнения (5.3а) получим, умножив обе его части на ,

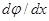после чего оно превратится в:

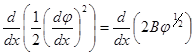(5.4)

Откуда следует:

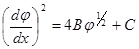(5.5)

В случае 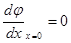постоянная интегрирования С также обращается в нуль, следовательно имеем:

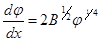(5.6)

Интегрируем затем (5.6), преобразовав его

после чего получим:

(5.7)

где при принятых условиях: U=0 при x=0, постоянная интегрирования также приравнивается нулю. Таким образом имеем окончательный ответ:

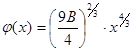(5.1.8)

Подставляя теперь в (5.8) значение B, перепишем его:

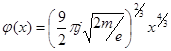(5.9)

Имея в виду, что при принятых условиях, потенциал второго электрода равен разности потенциалов между пластинами ( 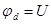), выразим, используя (6.1.9), плотность тока, проходящего через диод с расстоянием d между электродами при разности потенциалов U между ними:

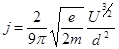(5.10)

Выражение (5.10) называется законом Чайлда-Ленгмюра или законом «3/2».

Если U выражено в Вольтах, j – в Амперах и d – сантиметрах, то «Закон 3/2» будет выглядеть следующим образом :

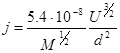
M – масса частиц в единицах протонной массы. В частности для электронов M=1/1840 и выражение примет вид

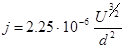
5.2. Плоский слой

Перейдем теперь к исследованию стационарной ситуации при которой поток холодных ионов (T_i= 0) плазмы идет на стенку вдоль оси x, ускоряясь полем слоя (которое одновременно препятствует уходу электронов). Будем считать, что в точке x = 0 скорость ионов u_{i =} u₀ и плотность n₀ .

Используем, как и в предыдущем случае, одномерное уравнение Пуассона. Здесь нам придется учесть уже два сорта частиц, вносящих вклад в формирование плотности объемного заряда: ионы и электроны. Плотность ионов можно выразить с помощью следующих соображений : они ускоряются электростатическим полем при сохранении плотности потока .

Запишем для потока ионов закон сохранения энергии :

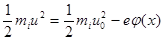(5.11)

и уравнение непрерывности:

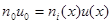(5.12)

Выразив затем из (6.11) текущую скорость ионов U(x) , получим с помощью (6.12) текущую плотность ионов:

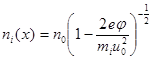(5.13)

Что касается электронов, то для них примем Больцмановское распределение:

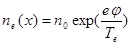(5.14)

Тогда уравнение Пуассона запишется в следующем виде:

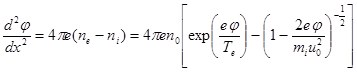(5.15)

Уравнение (5.15) можно переписать более компактно:

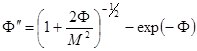, (5.16)

если ввести безразмерные переменные:

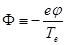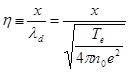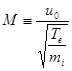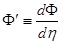; ; ; . (5.17)

Первое интегрирование уравнения (5.17) можно провести в общем виде, домножив обе его части на :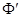

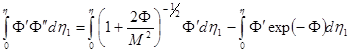(5.18)

Учитывая, что при 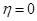, (поле в плазме отсутствует), получаем:

(5.19)

Дальнейшее интегрирование может быть выполнено только численно, однако и не производя его можно получить важный результат, проанализировав полученное уравнение (5.19). Видно, что его правая часть должна быть всегда положительна. Если рассмотреть область малых 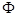( 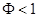), то, разложив ее в ряд по степеням 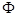и ограничиваясь членом второго порядка, получим условие существования решения уравнения(5.19):

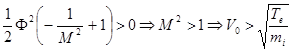(5.20)

Это неравенство называется критерием Бома, обуславливающим существование стационарного слоя в плазме. Для образования такого слоя необходимо, чтобы ионы, подходящие из плазмы к его границе, имели скорость, превышающую скорость ионного звука. Чтобы ионы в плазме могли набрать такую скорость, необходимо допустить существование электрического поля в области, предшествующей слою. Таким образом условие (5.20), полученное в предположении нуля поля и потенциала на границе слоя, строго говоря противоречат этим предположениям, которые могут быть теперь приняты только в качестве приблизительных. Можно предлагать различные формальные оправдания приемлемости проведенного рассмотрения от неопределенности положения границы слоя с плазмой до не вполне больцмановского распределения электронов. Физика же дела состоит в следующем: в слое плотность ионов всюду должна спадать медленнее, чем плотность электронов. При этом весь избыток положительного заряда окажется сосредоточенным вблизи стенки.

Если перейти теперь в область больших 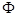( 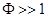), то плотностью электронов можно пренебречь и уравнение (6.16) будет выглядеть следующим образом:

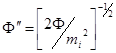, (5.21)

что с точностью до обозначений совпадает с использованным в предыдущем параграфе уравнением (5.3а), решение которого дает закон Чайлда-Ленгмюра для униполярного потока частиц в плоском диоде.

Проведенное рассмотрение дает возможность качественно описать распределение потенциала вблизи стенки состоящим из трех областей: предслоя – области в плазме с плавным нарастанием потенциала, где ионы набирают скорость, необходимую для формирования слоя – области, в которой происходит отражение основной массы электронов; размер этой области – несколько дебаевских радиусов и, наконец, области диода, размер которой определяется законом 3/2 при плотности потока ионов, определяемой скоростью рождения их в плазме. Разность потенциалов на этом диоде определяется необходимостью поддержания равенства потоков ионов и электронов на стенку.

5.. Плоский зонд

Полученный критерий можно использовать для оценки величины ионного тока насыщения, приходящего на плоский зонд, помещенный в плазму. Площадь собирающей поверхности зонда примем равной 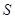; на зонд подан большой отрицательный потенциал, полностью препятствующий попаданию на него плазменных электронов и собирающий все приходящие на поверхность ионы. Как следует из полученного критерия, эти ионы имеют направленную скорость

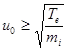(5.22)

Тогда ионный ток на зонд определится формулой:

(5.23)

где n_гр – плотность плазмы у внешней границы слоя. Определим положение этой границы, как места, где скорость ионного потока в точности равна скорости ионного звука. Для достижения такой скорости ионы должны пройти разность потенциалов 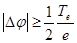, следовательно, граница слоя имеет по отношению к плазме отрицательный потенциал такой величины. Принимая электроны распределенными по Больцману, оценим их плотность в этом месте:

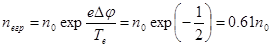(5.24)

Полагая плазму квазинейтральной, перепишем соотношение (6.1.23) с учетом (6.1.24):

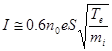(5.25)

С помощью этой формулы, измеряя ионный ток на зонд и зная температуру плазмы, можно оценить ее плотность:

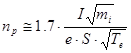(5.26)

Погрешности результатов вычислений по формуле (5.26) помимо неопределенности положения границы слоя обычно связаны с неопределенностью величины собирающей поверхности зонда.

5.4 Расходимость пучка заряженных частиц.

Рассмотрим плоский (ленточный) пучок заряженных частиц с зарядом q, массой m и энергией 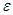движущихся в направлении z. Будем считать, что плотность потока однородна по сечению и, что в плоскости z = 0 скорости всех частиц направлены вдоль оси z . Его размер в направлении y считаем много большим, чем в направлении x.

Рис. 5.3. Форма огибающих расходящегося пучка. Заштрихованные прямоугольники – распределение плотности тока по сечению. a₀ - начальная полутолщина пучка, d₀ – полуширина (считаем ее неизменной).

Собственный объемный заряд пучка вызывает поперечное расталкивание составляющих его частиц. Уравнение Пуассона для рассматриваемого случая имеет вид

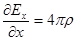(5.27)

где 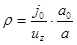, 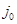- плотность тока в плоскости z = 0. а – текущая полутолщина пучка,

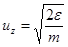- продольная скорость частиц пучка.

Откуда получаем величину напряженности электрического поля на границе пучка:

(5.28)

и записываем уравнение движения для крайней частицы, движущейся по огибающей:

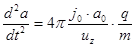(5.29)

Интегрируя (5.29) с учетом следующих начальных условий: a(0) = a₀ , 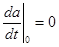, и принимая во внимание, что 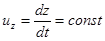(т.е. z = u_zt), получаем уравнение огибающей пучка:

(5.30)

или

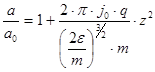
поскольку 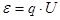, где 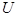- разность потенциалов, пройденная частицами пучка при их ускорении, то последнее выражение можно привести к виду

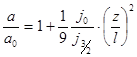(5.31)

где 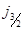- предельная плотность тока эффективного диода, в котором мог быть ускорен рассматриваемый пучок, а l - ширина этого диода.

Приложения

Приложение 1. Использованная и рекомендуемая литература

1. Д.А. Франк-Каменецкий, Лекции по физике плазмы,

Атомиздат , Москва 1968.

2. В.М. Кулыгин, «Начала физики плазмы», Москва, изд. МЭИ, 2001, (имеется в электронном виде)

3. В.М.Белокопытов, В.М. Кулыгин, «Элементы теории термоядерной плазмы», М: Изд. МЭИ, 2005, 84 стр.

4. Ф. Чен, Введение в физику плазмы, «Мир» , Москва, 1987.

5. К.Миямото, Основы физики плазмы и управляемого синтеза, Москва, 2007, Физматлит

6. В.Е. Голант, А.П. Жилинский, С.А. Сахаров, Атомиздат, Москва, 1977.

7. Сб. Вопросы теории плазмы, т.1, Госатомиздат, Москва, 1963.

8. А.Б. Михайловский, Теория плазменных неустойчивостей, т.1, Атомиздат, Москва, 1970.

9. Б.Б. Кадомцев, Коллективные явления в плазме, Наука, Москва, 1988.

10. А.А. Веденов, Задачник по физике плазмы, Атомиздат, Москва, 1981.

11. В.И. Ильгисонис и др. Сборник задач по физической электронике и физике плазмы, Москва, МИФИ, 2008.