ВЛИЯНИЕ ВНЕШНИХ ФАКТОРОВ НА ВЕЛИЧИНУ ЭЛЕКТРОДНОГО ПОТЕНЦИАЛА

Очевидно, что величина межфазного скачка потенциала должна зависеть от очень большого числа факторов. В первую очередь это химическая природа электродного материала, температура, концентрация и природа потенциалопределяющих частиц в растворе.

Данная взаимосвязь была установлена и носит название уравнения Нернста

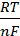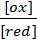Е = Е⁰ + ln . (9.3)

В этом уравнении Е – электродный потенциал (В); Е⁰- стандартный электродный потенциал (В); R = 8,31 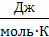универсальная газовая постоянная; Т-температура (К); n – число электронов в полуреакции; F – число Фарадея; [ox] – концентрация

окисленной формы потенциалопределяющих частиц (моль/л); [red] – концентрация восстановленной формы потенциалопределяющих частиц (моль/л).

Например, для полуреакции окисления

Mn²⁺+4H₂O - 5 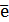= MnO₄^- + 8H⁺,(9.4)

в которой слева – восстановленная форма потенциалопределяющих частиц, а справа – окисленная форма, уравнение Нернста для стандартной температуры будет иметь следующий вид:

E = +1,507 + 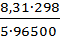ln .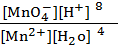

Введем несколько упрощений. При стандартной температуре 298К и переходе к десятичным логарифмам получим 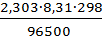=0,059В. Концентрация молекул воды в водных растворах может считаться величиной постоянной и в уравнение не включаться. В результате для стандартной температуры уравнение принимает следующий вид:

Е = Е⁰ + 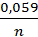lg 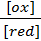, (9.5)

E = +1,507 + 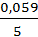lg .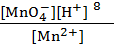

Подлогарифмическое выражение является константой равновесия (К) для реакции (9.4) К_с = 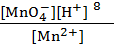, поэтому уравнение (9.5) может быть представлено в следующем виде:

Е = Е⁰ + 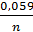lg К. (9.6)

Если электродная система состоит из металлического электрода, опущенного в раствор, содержащий одноименные ионы Me⁰ - 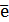= Me⁺ⁿ, то уравнение Нернста при стандартной температуре приобретает следующий вид, учитывая, что [Me⁰] – величина постоянная:

Е = Е⁰ + 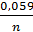lg [Me⁺ⁿ]. (9.7)

Взаимосвязь между константой равновесия и величиной ЭДС может быть получена из ур.2.9 и ур.9.6.

DG = - RT ln K и ΔG = -nFΔЕ.

Приравнивая правые части, получим

RT ln Kp = nFΔЕ,

откуда

ln K = .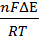

Для стандартной температуры и десятичных логарифмов

lgK = 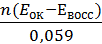. (9.8)

ЗАКОНЫ ФАРАДЕЯ

Использование электрохимичеких систем в технике возможно в двух вариантах.

1. Преобразование внутренней энергии самопроизвольных окислительно-восстановительных реакций в энергию постоянного тока. Это преобразование осуществляется в устройствах, называемых «химические источники тока».

2. Получение веществ за счет проведения несамопроизвольных ОВР под действием постоянного электрического тока. Эти процессы получили название «электролиз».

В обоих случаях существует взаимосвязь между массой реагирующих или образующихся на электродах веществ и количеством протекшего электричества. Эта взаимосвязь была установлена и носит название законов Фарадея.

1-й закон Фарадея: масса вещества, прореагировавшего или образовавшегося на электроде, пропорциональна количеству прошедшего через электролит электричества.

M ~ Q,

где m (г) – масса вещества; Q (Кл) – количество электричества.

Для перехода к уравнению вводится коэффициент пропорциональности q

M = qQ. (9.9)

Количество электричества Q определяется как произведение силы тока I (А) на время t (c).

m = q I t.(9.10)

2-й закон Фарадея: Теоретическая масса вещества, прореагировавшего или образовавшегося на электроде, при прохождении через него 1-го фарадея (F) электричества называется электрохимическим эквивалентом q.

q = 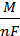(9.11)

где М (г/моль)- молярная масса вещества; n – число электронов в полуреакции; F(Кл/моль)- число Фарадея.

Объединяя аналитические выражения 1-го и 2-го законов получим

m = 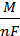I t B_т.(9.12)

В этом уравнении величина В_т называется «выход по току» и показывает долю тока, пошедшего на данную реакцию, если она протекала на электроде не одна. Определяется экспериментально, как отношение практически полученной массы вещества к ее теоретическому значению

В_т = 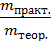∙100% . (9.13)

Если необходимо рассчитать объем образовавшегося в электродной реакции газа, то ур.9.12 может быть преобразовано

V = 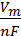I t В_т, (9.14)

где V_m (л/моль) – молярный объем – 22,4 л/моль.